task17

[TOC]

1. MX-X12H - 地铁 [E]

题面

给定 ，你有一张 的格点图，你需要构造 条折线，使得这些折线都只包含 LRUD 中两种垂直的方向

你需要使得每个点都被至少一条折线覆盖，求最小的 ，并且要求构造方案

对于仅求最小 的数据： 组询问，

对于要求构造的数据： 组询问，

题解

Sol

每条折线要么是左上到右下，要么是左下到右上，不难发现我们可以将其延长到四个角上

设 出发了 条到 ， 出发了 条到

那么最多覆盖的点数有一个上界：左上角和右下角边长为 的等腰三角形显然最多一共有 个点，另一边同理有 个点，而中间的部分两边会重复 个点，那么我们能覆盖的点数应该不超过：

$$y(n+m-2y+1)+x(n+m-2x+1)+x(x-1)+y(y-1)-xy\\=(m+n)(x+y)-x^2-xy-y^2$$

减去一个 后这个式子应该 ，我们称这个为 的判别式

可以猜测一下这个就是充要条件，写一下可以发现这是对的，注意到 越靠近越优，我们就能通过仅求最小 的部分分

接下来考虑构造。

经过充分长时间的手模，可以发现如下事情：

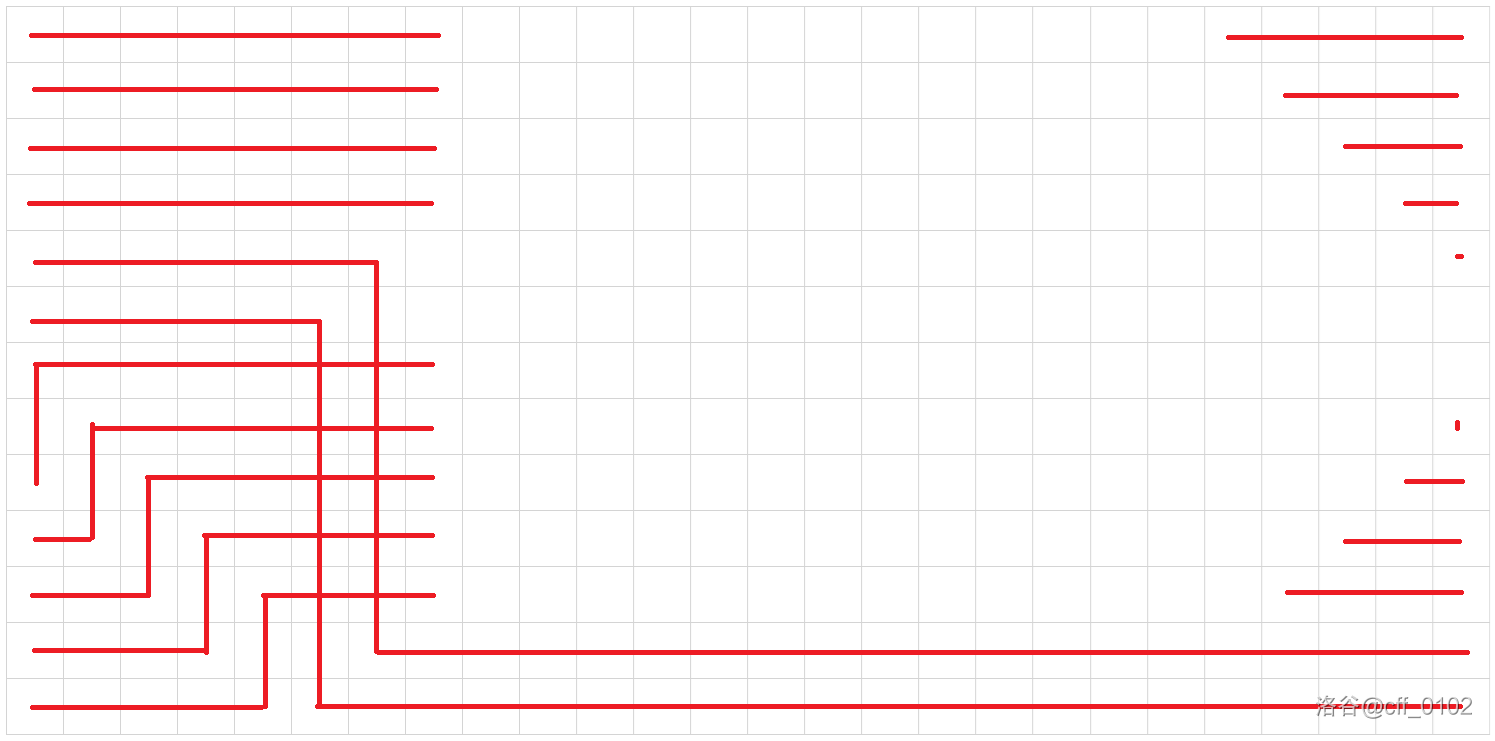
不妨假设 ，那么推一下式子可以发现 ，因此不妨假设 ，一定有

我们可以通过上面的操作把 减去 ，原问题会变成一个 的子问题

带入判别式求值发现 ，所以归纳构造即可，边界条件是 ，这时候是容易构造的

---

2. AGC020F - Arcs on a Circle [E]

题面

一个长为 的环上随机放 段弧，第 段弧的长度为 ，保证 为整数，每个弧被均匀独立随机地放在圆上的某个实数位置

求每个点都被弧覆盖的概率，输出浮点数

题解

Sol

首先我们可以把最大的 放在序列开头，断环成链

如果我们已经确定每个弧放的位置的整数部分，那么这个弧一定会覆盖一段 的长度，而它能不能覆盖一个小段就是检查不同弧之间的小数部分大小关系

因此，只要我们能够提前得知小数部分的大小关系，我们就可以转化成整数上的问题，而小数部分的大小关系可以提前枚举

枚举大小关系之后我们列一个 dp 状态： 表示考虑了前 个值域上的位置，当前选完的区间覆盖到的最远右端点为 ，并且使用的区间集合是 ，转移可以做到

复杂度

---

3. 集训队互测 2023 - 森林游戏 [E]

题面

给定一棵 个点的有根树，根为 ，点有正整数点权

两个人在上面博弈，每次每人选择一个没有父亲的点，将其删除，得分为自己删除的所有点的点权之和

两个人都要最大化自己的得分，求最优策略下先手的得分

题解

Sol

不会做，所以考虑大胆一点。首先把点权变成先手减去后手。

我们直接仿照树上打怪兽的贪心，每次选点权最大的点出来，认为它一定是紧跟着它父亲后面操作的。

但是有一点问题：我们合并完的点可能有两种，一种是选完会改变先后手，另一种是不会改变的

如果选完不会改变先后手，且它的点权还是正的，那么不管是谁操作，都一定会取这个点，这个看起来就很对，所以可以考虑直接和上面合并。

否则如果选完不会改变先后手，且它的点权是负的，那么这个东西就很没用，我们把这种东西放到最后合并

如果选完会改变先后手，那么我们就按点权从大到小合并

具体地，我们按照如下规则给点安排顺序：

• 首先是点权非负，且不会改变先后手的点，这些点按照权值从大到小排序
• 然后是会改变先后手的点，这些点按照权值从大到小排序
• 首先是点权为负，且不会改变先后手的点，这些点按照权值从大到小排序

每次选出最优先的点和父亲合并即可，正确性不知道

复杂度

---

4. QOJ4212 - Brackets [E]

题面

给定一个长为 的序列 ，其中 每个恰好出现两次

请构造一个字典序最小的长为 的合法括号序列 ，使得 相等的两个位置在 中也相等，或者判断无解

题解

Sol

贪心：我们从前往后扫，如果将当前这个填成 ( 后存在后缀和 ，说明不能这样填，我们就填 )，否则就填 (

如果构造出来解了，那么显然这个解是最大的，否则我们可以说明原问题即无解

证明：令 表示与 位置 值相等的另一个位置，不妨假设

如果我们没有构造出来解，我们找到任意一组合法解，从左到右扫每一组相等位置的取值，找到第一个不同的位置，这个位置只能是我们的解构造了 (，而合法解构造了 )

此时我们要说明：我们可以调整合法解使得这个位置取了 )

设这个位置为 ，我们可以把合法括号串的判定看成每个左括号去匹配一个它右面的 位置

不难发现我们可以调整 中的相等对匹配的位置，使得它们匹配是合法位置中最严的

此时我们找到贪心解中 匹配的位置，假设它在合法解中匹配的是 ，那么 一定可以匹配 匹配的元素，也就是说我们可以把 换成

因此上面的贪心就是正确的，复杂度

---

5. ARC138F - KD Tree [E]

题面

给定一个 的排列 ，定义 个点，第 个点为

你会给一个集合 的点安排顺序，安排顺序的过程如下：

• 如果 ，那么只有一种安排顺序的方式，直接返回
• 否则，你可以选择一个 ，将所有横坐标 的放在前面递归安排顺序，剩下的东西放在后面递归安排顺序，或者选择一个 ，将所有纵坐标 的放在前面递归安排顺序，剩下的东西放在后面递归安顺序

题解

Sol

对第一步操作进行容斥。

我们选择一个操作的集合 ，认为它是第一步就可以操作的，那么这些操作会把平面切成若干个小矩形

那么可以发现，我们对点的要求就是如果我们把有点的小区域染成黑色，黑色应该是从左下不断向右上移动的

对这个跑 dp，我们强制一个路径是从左下出发，走到右上角，然后在两个黑色之间必须向上再向右

定义两个状态，一个 表示向上走， 表示向右走，假设我们要求矩形 的答案，固定 后 和 都只有三维，转移是 的

总复杂度

---

6. CF1710D - Recover the Tree [E] ⭐

题面

对于一棵 个点的树，对于每个 ，你知道编号在 内的点是否形成一个连通块

请构造一棵树，使得其满足条件，数据保证有解

题解

TBA

---

7. 集训队互测 2023 - 雷同 [E] ⭐

题面

给定 个物品，每个物品有两个属性 ，其中 由输入给定， 初始为

你每次可以指定两个物品 ，将它们合并，合并会花费 的代价，合并完之后新的 为 ，新的 为

求将所有物品合并到一起的最小代价

多组数据，

题解

Sol

合并过程是一棵二叉树，最后的贡献上是 ，其中 为深度

不难发现如果将 升序排序之后， 一定是递降的，而 确定之后，后面 带来的贡献就只和树的形态有关

那么我们只要能够对于一个固定的 值，快速求出最优的合并方式，使得 的贡献尽可能小

容易发现这是一个 从大到小合并的过程，每次我们会加入一些新点，然后将这些点匹配，从 个点变成 个点

最优的匹配方式就是按照优先深度大的互相匹配，因为可以注意到我们留到后面的子树一定 越小越优，而其它合并方式都会被深度大的贪心匹配偏序掉，所以这样就是最优的

在这种情况下，我们可以列出 dp 状态： 表示考虑完前 个 ，当前还有 个节点，一种转移是合并掉一层，从 转移到 ，另一种是加一个点，加的新的点会产生 的 值贡献

复杂度

---

8. 集训队互测 2023 - Permutation Counting 2 [E]

题面

给定 ，求有多少 的排列 使得：

对所有 求出答案，对给定质数 取模

题解

Sol

对两个限制同时容斥，那么相当于序列被分为了 和 个上升段

从小到大加入数，相当于我们有 个数组，我们需要选择一个 ，满足 ，每次递增地将它们加入到这 个数组中

方案数也即：

$$\sum_{a_1+a_2+\cdots+a_y=n-y}\prod_{i=1}^k\binom{a_i+x-1}{x-1}$$

可以用范德蒙德卷积发现这就是

但是这样会有些段是空的，那么再做一遍二项式反演即可

最后代码写出来就是 算一遍组合数，然后做四次二项式反演，很有意思。

复杂度

---

9. 集训队互测 2023 - 没有创意的题目名称 [E]

题面

给定一个正整数 和一个长为 的序列 ，求有多少长为 的整数序列 满足如下条件：

• 对于所有 ，
• 对于任意 ，都有 （我们认为 的位置都满足 ）

答案对 取模

题解

Sol

放弃思考，相信打表。

当 的时候答案为 ，所有合法的序列形如选择两个数 ，然后 后 内的数一直循环

的时候所有合法序列为选择三个数 ，然后先是 ，之后还是 个一循环，但是循环节内每个数可以选择加上若干倍的 ，使其仍然不超过

的时候，不妨设 ，那么所有合法的序列为，选择一个 ，然后 个一循环，循环节如下：

• 如果 ，循环节为
• 否则循环节为

循环节 位置上的数均可以加上若干倍的 ，需要满足仍然不超过

之后只要统计不超过 的限制方案数即可，复杂度可能可以做到 ，但 跑的太快了，我也懒得管了。

---

10. 集训队互测 2023 - 挑战积和式 [K] ⭐

题面

给定一个长为 的数组 ，请选择一个长为 的整数序列 满足 ，求最大的 的值

题解

Sol

设最优解的和为 ，积为 ，那么其中的一个元素 删掉换成 之后会变成 ，这样调整不优当且仅当 ，也就是说最优解的 应当

而 的数最多选 个，那么我们设一个状态 表示选了 个数，乘积为 的最大和，这样我们就获得了一个 的做法

但是这个还是太高了。

最后复杂度里不能带 ，因此我们可以考虑能不能怎么把乘积分成两半最后合并起来

引理：对于任意非负实数集合 ，满足 ，，一定存在一个子集 使得

证明：

• 如果 ，那么我们直接选 为这个最大的元素即可
• 否则我们将 的大小补到偶数，然后从小到大排序，取所有排名为偶数的数作为 的元素，此时 显然 ，而我们将 去掉之后可以说明其一定 ，即

那么我们的值域只用保留到 ，最后将两个数组合并起来可以用凸包做到线性

注意到我们上面的说明中只用到了 和 ，那么我们可以对选的个数快速幂算出，每次转移依然是调和级数的

那么总复杂度就是

---

11. CF1707E - Replace [E] ⭐

题面

给定长为 的数列 ，定义函数 ：输入一个区间 ，返回

次询问，每次给定一个 ，求 迭代多少次之后会变成 ，或者判断永远不会变成

题解

Sol

注意到如果两个区间 ，那么 ，且

证明是容易的。

那么我们就可以选择一些关键区间，然后倍增处理出这些关键区间经过若干步之后的结果，最后合并起来

具体地，我们预处理 表示 经过 步之后变成了哪个区间，这样每个询问区间都可以拆成两个关键区间，那么我们询问就是 的

总复杂度

---

12. CF793E - Problem of offices [S]

题面

给定一棵 个点的树，根为 ，给定四个节点 满足它们均为叶子，且两两 lca 为

现在取一个欧拉序将其循环无穷多遍，是否可能满足：

• 任意两次相邻的 出现之间间隔的其它叶子个数相等
• 任意两次相邻的 出现之间间隔的其它叶子个数相等

题解

Sol

设两个变量 ，分别表示 间的叶子个数和 间的叶子个数

可以发现每个子树是否要对 进行修改是独立的，因此可以分开跑两遍背包

复杂度 或 或

---

13. UNR6 - 小火车 [K] ⭐

题面

给定 个整数 ，求一个长为 的序列 ，满足 ，且

保证 。

题解

Sol

我们的问题实际上就是要找两个子集和相等，而 保证了一定存在这样的子集

在值域上二分。时刻维护一个区间 ，表示和在这个区间内的子集个数 ，每次从中间分开两边至少有一边个数大于长度

求子集和在一个区间内的数量可以折半+双指针

复杂度

---

14. CF1483E - Vabank [E]

题面

你想从银行里贪钱。

你每次操作可以指定一个正整数 ，表示你要从银行里贪 的钱。

银行有一个阈值 ，如果 ，那么你会得到 块钱，否则你会被罚 块钱，如果你的钱数 ，那么你会被警察抓走

你初始有一块钱，请在不被警察抓走的前提下， 次操作内求出 的值

题解

Sol

首先依次询问 ，如果被罚钱了立刻停止，这样我们就知道了 在 内

然后我们在这个区间内二分，假设我们现在知道了 ，我们找到 的中点 ，如果钱数不够 就一直询问 ，够 之后就可以询问

这样分析一下次数可以发现是 的，总共是 ，还是太大了

改变一下我们的策略，可以发现我们最劣的情况是 等于当前二分的左端点 ，这种时候我们每次询问 都会失败，钱都会变得很少，因此一个简单的想法就是我们将询问中点向左调一下，但是要怎么调呢？

由于我们是倍增二分，我们可以假设 是远大于 的，所以我们直接将任意剩下来的 量级的钱忽略不计

这时候我们的钱一定是 的形式，而注意到 ，所以我们可以将 变到

也就是说，我们将 看作 ， 看作 ，我们就可以得到当前的钱数大于多少倍的 ，而这个已经可以记到 dp 状态里了

令 表示长为 的区间，当前钱数是 的 倍，最少的最坏情况询问次数

翻转一下状态和值，可以得到一个 的 dp，运行这个 dp 我们就可以求出在这个假设下，一个区间长度的最少询问次数

每次按照 dp 告诉你的最优转移点去询问即可，实际数据里跑出来是 次询问，比官解稍劣一点。

---

15. KTSC2025 - 진화 2 / evolution 2 [E]

题面

给定一棵 个点的有根树，点有点权 ，满足 为 到 的排列，且父亲的权值小于儿子的权值。

你可以向交互库提出询问，每次给定两个整数 ，交互库会回答 是否成立

设树结构一共有 种可能的点权序列符合条件，你需要在 次操作内求出所有 的值

题解

green:Sol

考虑一些极端的情况：

如果整棵树是一条链，那么 ，我们需要立刻确定答案

如果整棵树是一条链，再拼上一个点，那么 ，我们需要把这个点放到序列里二分

进一步地，如果整棵树是两条链，长为 和 ，那么 ，我们需要将两个序列通过某种方式归并起来。

而我们发现，如果我们能在 次操作内归并两个序列，在原树上就直接可以将其变为一条长为 的链，这样总的 就除掉了 ，也就是说我们可以在 次操作内解决整个问题

归并两个序列我写的是，设 ，每次找到 序列中的中点，二分出其在 中的位置，然后将 序列各分为两半左右递归，这样能获得 分

注意到这种策略比较劣的情况是 和 比较接近的情况，此时我们可以 次操作直接归并

把 的情况判掉就可以通过了。

---

16. ARC199D - Limestone [K] ⭐

题面

给定 ，有一个初始全 的 矩阵 ，你可以不断将某一行的前几列赋值成 ，或者不断将某一列赋值成 ，求对于所有能得到的矩阵 ， 中所有元素之和的和是多少，答案对 取模

题解

Sol

考虑最后一行的状态，为了唯一计数，不妨假设我们是把第一段极长的 用行操作染掉了，那么右边会有一些额外位置是 ，这些位置必须一整列都是 ，那么我们就可以将这列删掉

即，我们枚举一个 ，分别表示极长 段的长度，和右边有多少 ，算一些系数从 转移过来

注意到可以不枚举 ，提前预处理系数，总复杂度

---

17. ARC199A - Flip Row or Col 2 [K]

题面

给定一个大小为 的 矩阵，以及两个序列 ，保证 ，请合适地进行若干次行或列取反操作，使得第 行的 的个数为 ，第 行 的个数为

给出构造或判断无解

题解

Sol

注意到我们可以 ban 掉第一行的操作，不改变答案。

将第一行消为 ，此时我们至多进行 次列操作，对于剩下的每行，如果其 的个数 ，那么我们必须将行取反，否则必须不能取反

那么现在我们就没有行操作了，每一列 的个数必须是 或 ，相应地执行操作即可

复杂度

---

18. EC Final 2018 - Exotic … Ancient City [E/K] ✔️

题面

定义一个 个点的无向图，给定 个三元组 ，表示对于所有 ， 和 之间有一条边权为 的边

对每个 ，求只保留前 列点的图上，最小生成树的权值是多少，保证有解

题解

Sol

注意到 很小，最小生成树有一个求法是对每个 ，保留边权 的边，根据形成的连通块数就能判断出来最少连多少条 的边，全加起来就是最终答案

首先外层枚举一个 ，然后下面我们需要解决的就是加边，每个前缀的连通块数

如果暴力的话，我们就只需要用并查集不断维护出上一行的连通性，然后加上这一层的边，就知道有多少边是有用的，进而能够推算出连通块数

进行优化。

首先考虑如何从上一行的连通性推算出下一行的连通性，可以发现两个点 若能只通过 行的边联通，那么 也能只通过 行的边联通

考虑从第一行逐次扩展联通性的过程，第一行到第二行时，我们需要将 连向的所有 的点合并起来，这会在联通性上加一些边

而加的这些边，在第二行扩展到第三行的时候，就相当于我们需要把边端点的两个集合合并，从而又会新加一些边，这样不断扩展下去即可

而一共只会加 次边，因此使用并查集，复杂度是可以均摊的。

接下来考虑求出每一轮加的边有哪些是有用的，这个我们可以再维护一个并查集，有 个点，初始我们将所有 加入到并查集中，每次我们加一条边 的时候，就在 加一条边，此时可以通过两个并查集的连通块个数推算出有用的边数

总复杂度

---

19. AGC049F - Happy Sequence [K] ✨

题面

给定三个长为 的非负整数序列 ，你需要求一个对 中每个元素进行修改，使得对于任意 ，都有

将 修改为 会花费 的代价，需要满足 也是整数，求最小代价和

加强版：

题解

Sol

太魔法了。

将 排序

可以观察到最后的序列需要满足 ，也可以观察到

可以猜出一个性质：题目条件等价于，且

虽然不用这个性质也能做，但是用了会方便一点，称 ，

证明：

我们可以证明，

首先证明 取到的 满足 的 数量相等：画出 的折线，那么 一定开始结尾均斜率为 ，且在 向右移动的过程中，遇到一个 会使斜率 ，遇到一个 会使斜率 ，且开头结尾斜率都为 ，因此所有极小值的位置一定是某个斜率 的位置，也就是说 的 数量相等

然后证明 取到的值一定对应某个 ，满足 的 数量相等：考虑 的极小值位置 ，必然有 ，因此取 满足条件

最后可以验证当 的 数量相等时，由于 ， 和 的值确实是相等的，因此得证

接下来我们都用 考虑问题。

分析操作的性质，由于代价函数是凸的，所以我们可以直接将操作拆成代价为 的小操作

如果存在 ，且 的操作，那么我们把这两个操作删了一定更优

也就是说我们的操作一定满足存在一个分界点 ，使得 左边的东西都向右， 右边的东西都向左

此时可以发现，考察所有操作对每个位置的 值的改变， 是被增大最多的

进一步地，考虑最靠右的向右点 ，和最靠左的向左点 ，那么 内部都是被增大最多的 ，而最后这其中一定存在一个 满足 ，否则我们可以将 操作同时删去 ，仍然合法

而被增大最多却还是 ，说明这段区间一定是包含初始 的最小值的，因此我们可以找到最开始的最小值 ，然后将 左和 右分为两个单向的子问题

而对于单向的子问题，考虑固定一个代价 ，把所有 的操作全做掉，然后将每个点看作从此时的出发点，可以向左退掉一些步或向右多走一些步的双向问题，此时上面的结论依然是成立的，所以可以继续下去分治，每层代价范围会减半

总复杂度为

---

20. QOJ9080 - Item Exchange [K] ⭐

题面

有 个人，初始第 个人有物品 ，并且每个人都有一个 的排列 ， 表示第 个人对第 个物品的喜爱程度

你需要进行若干次如下操作，使得第 个人拥有第 个物品：

• 选择两个相邻的人 ，满足这两个人都更喜欢对方手上的物品，然后交换他们的物品

求是否可能达成， 组数据

，保证 的数据不超过 组

题解

Sol

注意到，每个人手上的物品一定是越变越喜欢的。

注意到，每个物品一定要么向右要么向左。

假设 ，注意到，找到最后一个向左的位置 ，那么 的位置一定不会动，并且中间一定有恰好 个向左， 个向右，并且我们如果确定了哪些点向左，进行的交换集合就是固定的

此时我们就有 的做法了，但我们性质还是太少了，难以优化

继续观察：对于任意一个 ，我们发现如果固定了它的方向，那么它在任意可行解内向左/向右走到的点都是唯一的

以向左的情况举例，那么 必定发生过一次交换，我们找到最大的 满足 ，且 中 比 优， 中 比 优，则 一定要在 处交换

假设 在某个 位置交换，显然 ，那么 都一定先被 经过后被 经过，也就是说 优于 ，而 中必须 优于 ，否则无法交换，因此上文中的 是唯一可以交换的位置，不存在则该物品无法向左

对于向右的情况同理。

现在我们知道每个 可以向左走到 ，或者向右走到 ，每个 只有两种情况，这启示我们使用 2-sat

考虑加哪些限制。

注意到选出来的方向一定满足 要互不相同，且 要互不相同，可以发现取值数加起来恰好为 ，那么我们只要让任意两个相等的最多选一个，最后一定会每种取值恰有一个

这之后，我们只要让每次交换都合法即可。

最后观察一个性质：对于 ，如果选择了 ，它们交换的位置是固定的

这是因为我们知道 相当于知道了 在所有向右中的排名，同理也知道了 在所有向左中的排名，它们交换的位置是可以推算出来的，即为

那么我们对每对 ，判断一下在 位置交换是否合法，不合法则连边限制它们不能同时取右左

可以发现这样如果有解，跑出来的解一定 两两不同，且每一步交换都是合法的，因此为合法方案

对每个 都做一遍，总复杂度

---

21. QOJ10042 - Scheduling [E/K] ✔️

题面

有 个区间 ，要求每个区间匹配到一个 中的位置 ，并且要求任意两个 绝对值之差 ，给出构造或判断无解

题解

Sol

如果没有不能相邻的限制，那么这个是容易的：我们只要从左到右扫，每次取出右端点最小的位置将其匹配掉

考虑强行改一下上面的做法，我们维护两个集合 ，分别表示第 个位置选和第 个位置不选，得到的右端点集合，那么会有转移：，前一种是好办的，后一种涉及两个状态的比较，不是很好处理

但是尝试一下可以发现，我们按照任何一种看起来比较有道理的方式比较两个集合，最后都对了

具体地，我们可以证明如下结论：

• 对于任意一个状态 ，如果其存在合法状态，那么一定有一个集合能够全维偏序同状态的其它所有集合
• 对于 都存在合法状态的情况， 一定能全维偏序

upd：不会证。

这个直接写就是 的，瓶颈在于复制 ，那么额外维护一个 ，表示两个集合的交集，当我们需要执行一个复制给另一个时，我们就将两个都清空，将所有内容扔到 中，容易做到

---

22. QOJ11108 - Nocturne without a Moon [E] ⭐

题面

给定一个 的排列 ，求有多少四元组 满足 ，且

题解

Sol

设 ，其中 ，那么不难发现四个数可以拆成 的形式

把 反演掉，我们就是要统计有多少四元组 使得

注意到 或

对于 的情况，可以发现枚举 的时间复杂度是正确的，因此我们在每个前缀位置，统计前面每对 的出现次数，以及后面每对 的出现次数，即可复杂度做到

对于 的情况，我们枚举 ，会得到若干个区间，所求即为区间之间有多少对包含关系，可以二维数点做到复杂度

而反演的复杂度为 ，因此总复杂度为 ，可以通过

进一步地发现，其实原条件可以变成要么有 ，要么有 ，第一部分复杂度为 ，第二部分复杂度为 ，因此可以把复杂度平衡到

---

23. KTSC2025 - 멋진 구간 / maxsum [E] ⭐

题面

给定 个区间 ，定义一个下标区间 是合法的当且仅当存在一个长为 的整数序列 ，满足 ，且 的和与 的最大子段和相等

次询问，每次给定 ，求有多少 是区间 是合法的

题解

Sol

考虑得出一个区间合法的条件，一个 序列合法需要如下条件：

• 对于任意 ， 的和 ，对于任意 ， 的和
• 对于任意 ， 的和 ，对于任意 ， 的和
• 的和需要大于 和 的最大子段和

那么不难发现 内部一定全填 ， 外一定全填

因此条件写成前缀和的形式就是：

• 和 分别为前缀非严格最小值和后缀非严格最大值
• 是 中的最小值， 是 中的最大值，并且比较边界的情况只有
• 对每个左端点和右端点我们可以预处理出来前后的最大子段和，那么要求

第一个条件对每个 是固定的，可以提前预处理

这种子区间类的问题一般都考虑扫描线，那么我们对 扫描线

是最小值的条件限制我们对于对于一个 ，可能可行的 一定是 的后缀非严格最小值，而在此基础上 是最大值的条件就相当于限制了 一定在一个后缀内

而我们发现，在所有后缀非严格最小值中，一定是越靠左越容易满足第三个条件，所以第三个条件限制的相当于是我们取后缀非严格最小值的一段前缀

那么综合起来，可行的范围就是一段区间内的后缀非严格最小值

用线段树维护即可，支持将一些位置打开或关闭，区间给所有打开位置 ，查询区间所有位置和，容易做到时间复杂度 ，空间线性

---

24. KTSC2025 - 뗏목 제작 [K]

题面

对两个正整数序列 ，定义 为将 两个序列保持内部位置关系，任意归并起来得到序列 ，如下式子的最大值：

$$\max_{1\le l\le r\le|X|+|Y|}\min(Z[l:r])\times(r-l+1)$$

给定一个长为 的序列 和一个长为 的序列 ， 次询问，每次给定 ，求

题解

Sol

阅读了 wsc 老师的题解。

计算 的方式为选择两个子串 ，然后最大化

不妨假设我们进行了离散化，那么对每个值 ，我们求出 表示 中最大能选出多长的最小值 的区间

接下来对 考虑，我们取一个笛卡尔树上的区间 ，其最小值为 ，设询问为 ，分类讨论：

• ，此时我们只用考虑一个区间，即为 的区间，而这相当于求 ，最大的 的值，可以离线用李超树维护
• ，我们可以类似地预处理出所有笛卡尔树上的区间选 ，最大的 的值，然后进行一个二维数点即可
• 剩下两种情况是对称的，我们以 为例。

我们对 扫描线，那么我们就是要转移所有后缀最小值为 的情况

考虑维护每个 对应的最长区间长度 ，那么加入一个 时，我们首先会把 的位置能选的长度全部置 ，并且 的位置能选的长度都会 ，我们扫到一个以当前为 的询问时，就是查询所有 的后缀最小值的贡献，也就是满足 的这样一段后缀的

这个我们可以使用分块实现，对每个块建出凸包，时刻维护最优取值点，整块 最优取值点最多移动 步，整块置 可以通过额外维护初始凸包实现，散块直接暴力重构

可以做到复杂度 ，空间复杂度线性

---

25. AGC022D - Shopping [E]

题面

有一条街，可以被看成一条数轴上的 区域，Yui 一开始在 的位置

有 个商场，第 个在 的位置，Yui 需要在这个商场进行 时间的购物

Yui 只能通过电车在街上往返，最初电车 时刻从 出发，匀速行驶在 时刻到达 ，然后折返，在 时刻到达 ，这样循环往复

Yui 希望在 个商场均进行购物，最后回到 ，求最少需要多长时间

题解

Sol

我们访问一个商场的时候可能有多种模式：

• 从左到这个商场，购物完之后坐上车向左（コ）或坐上车向右（→）
• 从右到这个商场，购物完之后坐上车向左（←）或坐上车向右（匚）

注意到一个商场，无论我们是从左还是从右到达，我们购物完方向不变的时间是一样的，而转向的时间可能比这个优

假设我们选定了商场每个商场转向方向或者直行，那么首先第 个商场一定转向，而中间的商场 コ 和 匚 一定互相匹配，因为如果某次折返之后返回了开头，那么一定会再折回去，就等效于直行了

而如果我们转向的时间不如直行优，我们显然没有必要转向，因为在经过这个位置的时候我们就可以直接选择直行了

因此我们选一些较优的 匚 / コ 匹配，经过一些认真的计算可得我们每匹配一次总距离减小

问题转化为若干个位置，每个位置可以为空，并且有些位置可以选成 匚，有些位置可以选成 コ，要求尽可能多匹配

这个可以用反悔贪心做到线性

复杂度

---

26. luoguP12705 - 呃呃 [] ⭐

题面

给定一张 个点的简单无向图， 次操作，每次操作添加或删掉一条边，求图内有没有四元环

，边数

题解

Sol

汤圆太牛了。

首先考虑如何判断初始图是否可行。

枚举一个点 ，其所有邻点 的出边集合一定不交，否则形成四元环，这样我们可以建出邻接表然后枚举 的所有邻点的所有出边，最多会枚举 个之后即可判定完 点，因此总体是 的

考虑扩展一下这个做法支持加边删边。

我们维护一个集合 ，初始为 ，每次 check 一个点，如果不存在四元环就将其从 中删除，如果存在四元环则停止 check 过程，加边的时候我们把边的两个端点再加入

每次询问之后我们就拿出一个点进行 check。

这样是正确的，因为我们维护的实际上是当前图中任意一个四元环都至少有一个节点在 中的一个集合，而每次加边直接将新加的两个点加入 显然是正确的（事实上加一个点也是对的）

容易势能分析得出复杂度是 的

---

27. AGC025F - Addition and Andition [E]

题面

给定两个二进制数 ，其中 的位数为 ， 的位数为

进行 次如下操作：，，

求最后 的值，以二进制输出

题解

Flamire 做法

Sol

按位扫描，从低到高依次查看每一位。

维护一个长为 的时刻数组，每个位置为 ，表示这一个时刻从下到上进了哪些位

那么我们的规则就是：假设当前是第 个时刻，那么如果我们当前的值是 ，就进到下一位的 时刻，并将当前值清零，否则继续检查下一个时刻，如果发生进位就转移到下一个位的同时刻

注意到进位会让数字和变小，因此进位次数应该是均摊线性的

我们唯一不能暴力处理的操作就是 向后移动的操作，而这部分相当于是整体位移了一下，所以我们使用一棵线段树，如果当前的进位是 我们就查下一个 的位置，如果是 我们就查下一个 的位置

实现较复杂，复杂度

题解做法

Sol

每次进行这个操作并不是很好搞，因此我们换一个方向考虑。

这个操作相当于 在向前移动，然后会产生一些进位之列的奇怪操作，具体地，每次操作可以表示为：

枚举 ，如果 ，那么就向前进位，一直到进位停止为止

一个大致的想法是每个 影响的范围是不太相交的，就是后面的 追不上前面的 ，所以我们可以改一下操作顺序，先从大到小枚举 ，然后连续做 次进位，每次找到 的最低的 ，把它向前进

而我们的过程中大部分时候都会有进位，就可以保证复杂度，没有进位的情况只是当前我们要进 ，并且上一个位置是 ，而这种情况可以快速跳过，用栈维护所有不为 的下标即可

复杂度

---

28. AGC027E - ABBreviate [E]

题面

给定一个长为 的 ab 字符串 ，你可以不断进行如下操作：

• 选择一个子串 aa，将其替换为 b
• 选择一个子串 bb，将其替换为 a

求经过若干次操作能得到多少本质不同的字符串，答案对 取模

题解

Sol

做麻烦了，记一下题解做法。

注意到 的值模 不变，并且注意到 的串，只要有相邻字符相同即可操作成 a， 的串，只要有相邻字符相同即可操作成 b

因此我们判定一个 是否能通过 操作得到即为将 划分为 段，每段为单个字符或者存在相邻相同字符且 值对应

这个还是不是很好 dp，首先特判掉 中没有相邻相同的情况

然后我们发现，遍历 中每个字符，每次贪心地选最短的满足条件的段，最后会剩下一段，那么 可以匹配当且仅当我们能选出来这样 个段，并且最后剩下的段

必要性是容易的，充分性可以通过调整得到：

• 一般情况下我们都可以将剩下的段拼到 的最后一个字符对应的段中，唯一不可能的情况就是最后一个字符的段是单个字符，如 a，然后剩下的段是 babababa
• 这时我们往前找，找到最靠右的 的位置，那么这个位置靠右的段一定都是长为 的，我们把 及靠右的所有长为 的段放在最后几个字符匹配，然后将空出来的位置全加到包含 的段中就是合法的

这个是容易 dp 的，复杂度