task9

[TOC]

1. CF1375H - Set Merging [E] ⭐

题面

给定 $1\sim n$ 的排列 $a$，初始有 $i$ 个集合 $S_i=\{a_i\}$，计数器 $cnt=n$

你可以将两个值域不交的集合取并，具体地，每次你可以进行这样的操作：

$cnt\leftarrow cnt+1$
$S_{cnt}\leftarrow S_u\cup S_v$

当且仅当 $S_u$ 中的最大值小于 $S_v$ 的最大值

现在给出 $q$ 个目标集合，每个集合形如 $T_i=\{a_u|u\in[l_i,r_i]\}$

你需要进行若干次操作，并给出 $k_1,k_2,\cdots,k_q$，使得 $S_{k_i}=T_i$ 成立，你需要保证 $cnt\le2.2\times10^6$

$1\le n\le2^{12},1\le q\le2^{16}$

题解

Sol

这个值域不交的限制很怪，这限制了我们最后区间 $[l,r]$ 的集合一定是通过 $[l,r]$ 中值 $\le y$ 的元素集合，以及 $[l,r]$ 中值 $>y$ 的元素集合合并得到

那么我们不妨对值域分治，如果当前分治值域为 $L,R$，中点为 $M$，那么将 $[l,r]$ 中 $\le M$ 的数和 $>M$ 的数递归下去处理

注意到一个值域区间如果包含的数的集合相同的两个询问是可以合并起来的，我们发现这样合并之后复杂度就是对的。

具体地，一个值域区间 $[L,R]$ 最多会有 $\min(q,\frac12len(len-1))$ 个本质不同的询问，其中 $len$ 为 $R-L+1$

我的分析好像有点常数问题，所以我们贺一下 editorial 的。

不妨设 $n=2^N,q=2^Q$，那么我们需要计算的式子即为：

$\sum_{i=0}^N2^{N-i}\min(2^{2i-1},2^Q)$

对于 $i\le\frac Q2$ 的情况，式子即为：

$\sum_{i=0}^{Q/2}2^{N-i}2^{2i-1}=2^{N-1}\sum_{i=0}^{Q/2}2^i\le2^{N+Q/2}$

对于 $i>\frac Q2$ 的情况，式子即为：

$\sum_{i=Q/2+1}^N2^{N-i}2^Q=2^Q\sum_{i=0}^{N-Q/2-1}2^i\le 2^{N+Q/2}$

两部分加起来就是 $2n\sqrt q$，可以通过

2. CF768G - The Winds of Winter [S]

题面

给定一棵 $n$ 个点的有根树，对于每个点 $u$，如下定义 $f(u)$：

将 $u$ 从有根树中删除，形成一个森林，你需要删除一条边并加上一条边，使得这张图仍然是森林，$f(u)$ 为森林中树大小最大值的最小值

对每个 $u=1,2,\cdots,n$，求 $f(u)$

$1\le n\le10^5$

题解

Sol

对于一个 $u$，$f(u)=\max(mx^\prime,\min\limits_x(mn+|x-\frac12(mx-mn)|))$，其中 $mx,mx^\prime,mn$ 分别表示删掉 $u$ 后最大，次大，最小的子树大小，$x$ 为 $mx$ 的任意一个子树的大小，我们需要选取一个最接近 $\frac12(mx-mn)$ 的子树大小·

直接树上启发式合并即可。

复杂度 $O(n\log^2n)$

3. CF718E - Matvey’s Birthday [S]

题面

给定一个长为 $n$，字符集为 a~h 的字符串 $s$，按照如下方式建图：

在满足 $|a-b|=1$ 或 $s_a=s_b$ 的点 $a,b$ 之间建一条长度为 $1$ 的无向边

求任意两点间最短路的最大值，以及达到最大值的点对数

$2\le n\le10^5$

题解

Sol

考虑如何求两点间的最短路，容易发现要么使用 $s_a=s_b$ 的边，要么不使用 $s_a=s_b$ 的边

如果使用了，我们枚举使用的边满足 $s_a=s_b=c$，那么 $x$ 与 $y$ 之间的距离就为 $dis_{x,c}+1+dis_{y,c}$，其中 $dis_{p,q}$ 表示从第 $p$ 个位置出发，到一个字符为 $q$ 的位置的最小距离，这个是容易 01-bfs 求出的

但是枚举每个点对显然不行，因此我们考虑观察一些性质，注意到如果 $s_x=s_y$ 相同，那么 $|dis_{x,c}-dis_{y,c}|\le1$ 一定成立，也就是说对于一种字符的点，$dis_x$ 这一列的数最多有 $2^{|\Sigma|}$ 种情况，我们可以将字符与 $dis$ 均相同的数合并在一起

注意到我们还需要考虑不经过 $s_a=s_b$ 的边的情况，这种情况就是下标之差，因此我们对于每个等价类，还需要记一下最左出现和最右出现，那么我们就可以枚举等价类，求出等价类之间的距离最大值，也就可以解决第一问

考虑第二问如何处理，对于等价类 $(i,S)$ 和 $(j,T)$，假设他们的距离最大值等于答案，那么我们就需要求出取到最大值的方案数，注意到此时最短路长度相当于 $\min(|x-y|,val)$，其中 $val$ 是一个能通过 $S$ 和 $T$ 求出的常数，那么也就是求数组内距离大于某个定值的点对数，容易前缀和处理

总复杂度 $O(n|\Sigma|+(|\Sigma|2^{|\Sigma|})^2+|\Sigma|2^{|\Sigma|}n)$

4. CF1416F - Showing Off [E]

题面

对于一个 $n\times m$ 的正整数矩阵 $W$ 和 LRUD 矩阵 $C$，满足 $C$ 中没有字符指向矩阵之外，我们按照如下方式生成 $A$：

对于 $(i,j)$，$A_{i,j}$ 的值为从 $(i,j)$ 出发，能走到的所有格子的 $W$ 值之和

现给定 $n\times m$ 的矩阵 $A$，你需要还原出任意一个 $W$ 和 $C$，或判断无解

$1\le n\cdot m\le10^5,2\le A_{i,j}\le10^9$

题解

Sol

这个图最后一定是一棵基环树，而注意到这张图里所有的环都是偶环，所以任意一个环都可以拆成若干个长度为 $2$ 的环

对于存在一个相邻的 $A$ 值小于它的 $A_{i,j}$，我们直接将 $(i,j)$ 指向这个格子，那么显然可以保证 $(i,j)$ 能够满足要求，因此我们只需要考虑不存在相邻 $A$ 值小于它的格子

这样的格子一定在环上，也就是说它们一定要和一个相邻的格子形成长为 $2$ 的环，这看起来很像匹配，那么我们现在要解决的问题就是：

给定一张二分图，一些左部点和一些右部点为关键点，构造一个匹配使得每个关键点都被匹配上

Flamire 做法

加入一些非关键点，把两边的点数补到一致，再在所有非关键点之间两两连边，这个图满流当且仅当原问题有解，方案是容易构造的

两两连边可以建图优化掉，复杂度 $O(nm\sqrt{nm})$

题解做法

首先保留左部关键点和右部点跑最大匹配，然后保留左部点和右部关键点跑匹配

我们声称：两张图都能满流当且仅当原问题有解

按如下构造方案：

直接把最大匹配看成从关键点到匹配点的有向边，将两个图的边连到同一张图上，那么每个关键点的出度一定恰为 $1$，每个非关键点的出度一定恰为 $0$

这张图上每个点入度和出度都不超过 $1$，因此会产生若干链和环，对于环我们直接 dfs 交替匹配即可，对于链我们从链头（入度为 $0$ 的一端）开始匹配，每次将链头两个匹配起来，这样可能会舍弃最后一个点，但最后一个点出度一定为 $0$，因此舍弃不会产生影响

总复杂度 $O(nm\sqrt{nm})$

5. CF1558F - Strange Sort [S]

题面

给定一个 $1\sim n$ 的排列 $a$，保证 $n$ 为奇数，按照如下进行若干轮操作：

如果当前为第奇数轮操作，对于所有 $i=1,3,5,\cdots,n-2$，如果 $a_i>a_{i+1}$，那么交换 $a_i,a_{i+1}$
如果当前为第偶数轮操作，对于所有 $i=2,4,6,\cdots,n-1$，如果 $a_i>a_{i+1}$，那么交换 $a_i,a_{i+1}$

求多少轮后 $a$ 被排好序

$3\le n\le2\times10^5$

题解

Sol

注意到排好序相当于对每个 $m$，$\le m$ 的数都在最前面，那么我们对于一个 $m$ 考虑，将排列变为 $01$

手模可以发现，如果我们设 $tim_i$ 表示第 $i$ 个 $0$ 到达第 $i$ 个位置的时间，那么有递推式 $tim_i=\max(x_i-i+[2\nmid x_i],tim_{i-1}+1)$，其中 $x_i$ 表示第 $i$ 个 $0$ 的初始位置，并且在 $x_i=i$ 时 $tim_i=0$

那么我们要求的答案就是对于所有 $m$，最后一个 $0$ 的 $tim$ 最大值

最后一个 $0$ 的 $tim$ 可以用 $\max_{x_p\neq p}(x_p-p+[2\nmid x_p]+b_p)$ 来计算，其中 $b_p$ 表示第 $p$ 个 $0$ 后面还有多少 $0$

从 $m$ 到 $m+1$ 相当于每次添加一个 $0$，上述式子是容易用线段树维护的

复杂度 $O(n\log n)$

6. CF713E - Sonya Partymaker [E]

题面

一个长为 $m$ 的环，上面整点依次标号为 $1\sim m$，初始每个整点处都有一把椅子

有 $n$ 个人，第 $i$ 个人初始在 $a_i$，你需要给每个人分配一个方向（顺时针或逆时针），这个人会一直沿这个方向以 $1$ 的速度运行

任意时刻，如果某个人当前的位置上有一把椅子，那么她会立刻将这个椅子烧掉

求所有椅子都被烧掉的最小时间

$1\le n\le10^5,1\le m\le10^9$

题解

Sol

首先可以考虑二分，那么每个人能覆盖的位置是一个端点为 $a_i$，长度为 $mid$ 的一段区间，我们需要判断是否存在一种方案使得这些区间覆盖所有整点

考虑直线上的问题怎么处理：令 $f_i$ 表示最左边的 $i$ 个人最长能覆盖的一段连续前缀为多长，枚举第 $i$ 个人向左还是向右，容易做到 $O(1)$ 转移

考虑如何扩展到环上，扩展到环上主要的困难在于最右端可能绕回来影响最左端，这里有两种处理方式

Flamire 做法

考虑枚举第一个人的选择，不妨设选择了顺时针，那么我们以 $a_1$ 为零点，逆时针为正方向建立直线，此时最右端的人如果向右，有可能绕回最左端

讨论最后一个人的选法：

如果向右选，那么我们知道绕回的长度有多长，直接设到 $f_0$ 里然后转移即可
如果向左选，那么可以说明剩下的人再向右选跨过零点一定不优，也就是说没有人跨过零点，直接计算即可

复杂度 $O(n\log m)$

题解做法

注意到如果任意相邻两人之间空隙均 $\le mid$，那么一定有解

否则找到最大的空隙，其长度一定 $>mid$，也就是说以这个空隙的端点建立直线，一定不会产生回绕的情况

直接 dp 即可

复杂度 $O(n\log m)$

7. CF1148G - Gold Experience [K]

题面

给定 $a_1,a_2,\cdots,a_n$ 以及一个整数 $k$，保证 $2k\le n$

你需要从 $a$ 中选出一个大小为 $k$ 的子集 $S$，使得这个子集 $S$ 满足以下两个条件中的一种：

$S$ 中的元素两两 $\gcd$ 不为 $1$
对于任意 $x\in S$，存在一个 $y\in S$ 使得 $\gcd(x,y)=1$

$6\le 2k\le10^5,2\le a_i\le10^7$

题解

Sol

我们在 $\gcd=1$ 的数之间连边，那么相当于求一个独立集，或者求一个集合使得导出子图不包含孤立点

那么如果对每个点求一下度数，度数 $=0$ 的点数如果 $\ge k$，那么直接输出度数为 $0$ 的点即可

否则，至少有 $\frac n2$ 个点度数不为 $0$，我们手玩一下，可以发现无法构造的情况当且仅当剩下的点形成了一个匹配，而这种情况我们直接取度数 $=0$ 的点和匹配一边的点即可构造一个独立集

不是匹配的情况写一些愚蠢的特判就可以构造一个不包含孤立点的子集

现在问题是如何得知这个图的信息：

首先是求度数，这个可以对质因子容斥，即对每个 $\mu\neq0$ 的点，存有多少数是该数的倍数，然后对于一个数枚举一个质因子的子集，复杂度 $O(n2^{\omega(a_i)})$

其次我们需要求任意一个与某个数有连边的数，那么我们直接把上面的计数套一个整体二分，复杂度 $O(n\log n2^{\omega(a_i)})$

8. CF1368H - Breadboard Capacity [E] ✔️

题面

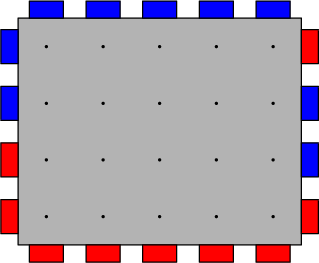
给定 $n,m$，有一个 $n\times m$ 的电路板，电路板的上下左右的每个格子外面都有一个颜色为蓝或红的元件，你需要将尽可能多对相同颜色的元件用电线接在一起，满足：

一个元件只能另一个同色元件连接
电线必须平行于电路板边界，且只能在图中格点（黑点）处转弯
电线只能在格点处相交，并且不能自交

H1：求最多连接多少对元件

H2：

$q$ 次修改，每次选定电路板的一个边界，以及一个区间 $[l,r]$，反转这个区间内的元件颜色

在所有修改前及每次修改后，求 H1 的答案

$1\le n,m\le10^5,0\le q\le10^5$

题解

Sol

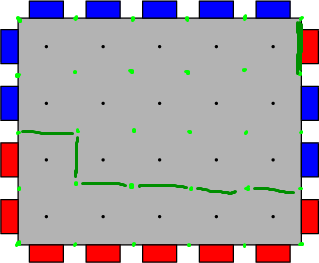
首先，这是一个最大流。直接连出一张网格图，然后将源点向一种颜色连边，另一种颜色向汇点连边

那么，这是一个最小割。也即我们需要在上图绿点之间连边，用最小的长度将蓝色元件和红色元件分开

考虑这个最小割有什么性质：

首先，不会有环，这是显然的。
其次，中间显然不会有奇度点，因为这样一定有一条边两侧区域的颜色是一样的，这条边可以删掉
那么我们可以将这个割看成若干条从边界出发走到边界的路径，而注意到如果一条路径的两条边界不相对，这显然是不优的，因为我们可以直接将其折到边界上，不增加代价，显然不劣
上一条也限制了我们的路径不能相交
那么现在割的形态形如若干条上边界到下边界的路径（也可能是左边界到右边界，不过这是对称的，下面均只讨论上下的情况），注意到这些路径一定是竖直的直线，因为否则我们可以将其折成一段竖直的，和一段贴着上边界或下边界的，这显然不劣
也就是说，割的形态一定是首先由若干条竖直的线从上边界到下边界，然后对于割开的每个连通块，再在边界上连边将某一种颜色的全部割出去

相当于我们选择若干分界点 $0=x_0<x_1<x_2<\cdots<x_k<x_{k+1}=m$，使得这个式子最小：

$\sum_{i=1}^{k+1}\min(cntR[x_{i-1}+1:x_i],cntB[x_{i-1}+1:x_i])$

其中 $cntR[l:r],cntB[l:r]$ 分别表示 $[l,r]$ 列内，上边界与下边界中有多少红色与蓝色，特别地，我们认为第一列包含左边界，第 $m$ 列包含右边界

这个不难用线段树维护，存一下左端点与右端点当前区域颜色即可，区间反转也是容易的，可以维护 $4$ 个矩阵，但观察一些性质可以只维护两个

复杂度 $O(n\log n)$

9. CF1583H - Omkar and Tours [S]

题面

给定一棵 $n$ 个点的树，每个点有一个权值 $e_i$，边有边权 $c_i,t_i$

$q$ 次询问，每次询问给定一个值 $v$ 以及一个点 $x$，你需要求出两个值：

设从 $x$ 出发，只走 $c_i\ge v$ 的边，能到达的点的集合为 $Y$，$Y$ 中节点最大 $e$ 值
设 $Y$ 中 $e$ 值最大的节点组成的集合为 $Z$，求 $x$ 到所有 $Z$ 中节点的最短路径上，最大的 $t$ 值

$2\le n\le2\times10^5,1\le q\le2\times10^5,1\le e_i,c_i,t_i,v\le10^9$

题解

Flamire 做法

Sol

第一问是好做的，直接离线并查集即可

考虑第二问，访问的边集相当于将所有 $Z$ 中的点，以及询问的 $x$ 拉出来建虚树，得到的所有边

那么我们在并查集的过程中维护一下虚树的点集即可，启发式合并容易做到 $O(n\log^2n)$

题解做法

Sol

第一问是好做的，直接离线并查集即可

考虑第二问，我们对 $t$ 建 Kruskal 重构树，那么相当于要找出 $x$ 与 $Z$ 中的点的最浅 lca

这只可能发生在 $Z$ 中 dfn 最小的点或最大的点，在并查集的时候维护一下这两个点即可

复杂度 $O(n\log n)$

10. CF1556G - Gates to Another World [K]

题面

对于 $0\sim2^n-1$，如果两个数满足它们的二进制只有一位不同，那么外面在这两个数之间连一条无向边

$m$ 次操作，每次操作为以下两种中的一种：

block l r，将 $[l,r]$ 内的点及其相关的边全部删除，保证一个点只会被删除一次
ask a b，查询 $a$ 和 $b$ 是否联通

$1\le n\le50,1\le m\le5\times10^4$

题解

Sol

不够信仰导致的。

首先显然可以时光倒流，然后考虑将区间放到 trie 树上，并且通过添加儿子使得每个节点要么有 $0$ 个儿子要么有 $2$ 个儿子

那么现在每个叶子都对应了一个区间，并且这个区间内部显然是联通的，也就是说我们只需要建出区间之间的边即可

可以按照如下方式构建边：

void link(int x,int y)
{
	if(leaf(x)&&leaf(y)){e.emplace_back(x,y,min(w[x],w[y]));return;}
	if(leaf(x))link(x,ch[y][0]),link(x,ch[y][1]);
	else if(leaf(y))link(ch[x][0],y),link(ch[x][1],y)
	else link(ch[x][0],ch[y][0]),link(ch[x][1],ch[y][1]);
}

当 $x$ 和 $y$ 都为叶子时我们插入一条 $x$ 到 $y$，边权为两个点被删除时间最小值的边

那么最后遍历一遍然后用并查集维护即可

分析一下这样做的边数：点数显然是 $O(nm)$，而每个点只可能在合并祖先的左右儿子的时候被访问到一次，因此总贡献的复杂度为 $O(n)$，也就是说边数是 $O(n^2m)$

至于为什么 $O(n^2m)$ 条边能用 vector 直接存下来，我也不知道。

总复杂度 $O(n^2m\alpha(n))$

11. CF983D - Arkady and Rectangles [K] ⭐

题面

给定二维平面上 $n$ 个矩形，按照顺序将第 $i$ 个矩形涂上第 $i$ 种颜色，后涂上的颜色会覆盖先涂上的颜色，求平面上有多少种颜色

$1\le n\le10^5$

题解

Sol

先离散化一下，我们很大可能要求出每个矩形最后有没有被覆盖。

一种很自然的想法是扫描线，如果直接时刻维护每个矩形有没有被覆盖会比较困难，因此我们考虑这样的思路：用数据结构维护出任意一个还没有被放到答案里的没有被覆盖的矩形，然后将这个矩形放到答案中，并对数据结构做修改

具体地，我们使用线段树维护这件事情，这相当于我们有值域个集合，每次操作会在一个区间加入一个数 $x$ 或者撤销之前的某次操作，我们需要找到任意一个集合，使得这个集合的最大值还没有放到答案中

我们的线段树每个节点维护三个东西：

插入到这个节点上的集合 $S$
只考虑这个子树内的插入，集合最大值的最小值 $mn$
只考虑这个子树内的插入，最大的没有放到答案中的集合最大值 $mx$

$S$ 不用 pushup，$mn$ 和 $mx$ 的 pushup 容易通过分类讨论实现，当我们发现根的 $mx$ 有值时我们将根的 $mx$ 标记并更新这个数在线段树上的所有出现位置（一个区间，也即 $O(\log)$ 个节点）

我们需要支持取出 $S$ 的最大值，因此需要用可删堆维护

复杂度 $O(n\log^2n)$

12. CF1237H - Balanced Reversals [K]

题面

给定两个长为 $n$ 的 01 串 $s,t$，保证 $n$ 为偶数

一次操作你可以选择一个 $s$ 的长为偶数的前缀将其 reverse，请你构造一个不超过 $n+1$ 次操作将 $s$ 变为 $t$ 的方案

$2\le n\le4000$

题解

Sol

我们可以将两个字符视为一个元素，以下下标均建立在这个假设之上

注意到我们操作 $i-1,i$ 产生的效果相当于将第 $i$ 个元素 reverse 后插入在序列前面

那么如果我们用这种操作完成的条件是 $00/11$ 的个数相等，并且 $s$ 中 $01/10$ 个数等于 $t$ 中 $10/01$ 个数

$00/11$ 个数显然无法改变，那么我们需要考虑的就是能否用一次操作将 $01/10$ 个数改对

定义 $f(s)$ 为 $s$ 中 $01$ 个数减去 $10$ 个数，那么我们期望的是 $f(s)=-f(t)$

如果 $|f(s)|\ge|f(t)|$，那么我们可以说明一定可以 reverse 一个 $s$ 的前缀来让 $f(s)=-f(t)$，具体地，$s$ 的前缀的 $f$ 值一定包含了 $0\sim f(s)$ 中的所有数，那么 reverse 这些前缀就能得到 $-f(s)\sim f(s)$ 中的所有奇偶性与 $f(s)$ 相同的数，又因 $f(t)$ 与 $f(s)$ 同奇偶，因此我们可以 reverse 一个前缀得到 $f(t)$

对于 $|f(s)|<|f(t)|$ 的情况，我们 reverse 一个 $t$ 的前缀即可，其含义就为操作完之后再操作一次前缀

剩下的用上述方法构造即可，复杂度 $O(n^2)$

13. CF1753E - N Machines [S]

题面

给定常数 $b,p,m$，以及一个长为 $n$ 的序列，每个序列为 +x 或 *x，其中 $x$ 是一个正整数

定义这个序列的权值为：初始令 $x$ 为 $1$，按顺序执行序列中每个运算，最后得到的数

保证初始序列的权值 $\le2\times10^9$

你每次可以花费 $p$ 的代价，选定一个 +x 操作，将其移到序列中的任意位置，或者花费 $m$ 的代价，选定一个 *x 操作，将其移到序列中的任意位置

求在花费 $b$ 的代价内能将序列的权值修改为多少

$1\le n\le10^6,1\le b,p,m\le10^9$

题解

Sol

注意到权值 $\le2\times10^9$ 的权值很强，限制我们最多有 $\log V$ 个不为 $1$ 的 *x

操作显然是将 +x 移到序列开头，或将 *x 移到序列末尾

我们将所有 +x 拿出来，那么这相当于我们可以选择后缀将其中的元素倍率乘上某一个值，或者选择元素将其倍率赋值为所有 *x 的乘积

那么如果 *x 和 *y 操作满足 *x 在 *y 前，且 $x\ge y$，那么我们在选择 *y 前一定要选择 *x

目测一下此时乘法的选取方式就不是很多了，看起来只有几千（实际上范围内最大只有 $4608$），那么我们对于每种选取方式直接求解

按所有 *x 的操作把序列分块，那么求解一种选取方案的答案时，就相当于每块有一个倍率 $w$，求每个块的元素乘上该块倍率得到的最大 $k$ 个，二分这个值然后对于每块二分求个数，可以做到 $O(\log^3)$

最后复杂度 $O(F(V)\log^2V\log n)$

14. CF1322E - Median Mountain Range [E]

题面

给定长为 $n$ 的序列 $a_1,a_2,\cdots,a_n$，每一个时刻这个序列都会产生如下改变：

对于所有 $2\le i<n$，同时将 $a_i$ 赋值为 $a_{i-1},a_i,a_{i+1}$ 的中位数

可以证明这个序列将在若干次操作后保持不变，求前多少次操作会改变这个序列，以及最后序列会变成什么

$1\le n\le5\times10^5,1\le a_i\le10^9$

题解

Sol

套用经典套路，转化成 $01$ 上的问题：我们只需要将 $\le m$ 的数变为 $0$，$>m$ 的数变为 $1$，那么操作次数就是所有 $m$ 得到的操作次数的最大值

对 $m$ 扫描线，注意到 $m$ 的操作次数可以从最长 $01$ 交替段求出，那么用线段树维护单点修改，全局最长 $01$ 交替段长度即可

考虑如何求最后的序列，对于每个 $a_i$，如果最后的序列中其为 $0$，那么可选择的 $m$ 是一个后缀，也就是说我们只需要维护出这个位置第一次变成 $0$ 的时刻就能求出这个位置最后的值

注意到单点修改时我们只会影响经过这个点的 $01$ 交替段，不难在线段树 pushup 的时候顺带维护，对答案序列的操作即为将区间内还没有答案的点，答案全部设为某个数，这个可以用并查集维护

复杂度 $O(n\log n)$

15. CF1396D - Rainbow Rectangles [K]

题面

有一个大小为 $L\times L$ 的矩形，上面有 $n$ 个 M&M，分别在第 $x_i$ 行和第 $y_i$ 列，颜色为 $c_i$，总颜色数为 $k$

求有多少子矩形满足这个矩形中 $k$ 种颜色都至少出现一次

$1\le k\le n\le2000,1\le L\le10^9$

题解

Sol

首先可以离散化。

显然有一个 $O(n^3)$ 做法：枚举上下边界，然后对右边界进行 two-pointers

考虑优化这个做法，two-pointers 的过程显然不太能优化，因此我们考虑移动下边界，快速维护出每个右边界对应的位置 $f_i$

加点非常困难，因此我们考虑删点，也即下边界从最下面向上移动，注意到如果我们删点的时候删掉了某一个颜色，那么设 $prv_i$ 与 $nxt_i$ 分别表示这个颜色前一次/后一次出现的位置，那么相当于我们将 $[i,nxt_i)$ 内所有 $f_j\ge prv_i$ 的点 $j$ 设为 $prv_i$

由于 $f$ 是单增的，这可以使用线段树实现

复杂度 $O(n^2\log n)$

16. CF1718D - Permutation for Burenka [E]

题面

定义两个长为 $n$ 的元素互不相同的数组 $a,b$ 相似当且仅当对于每个区间 $[l,r]$ 都有 $\text{argmax}(a[l:r])=\text{argmax}(b[l:r])$

给定一个 $1\sim n$ 的排列 $p$，以及一个数组 $a$，$a$ 中有 $k$ 个位置为 $0$

给定一个大小为 $k-1$ 的集合 $S$，$q$ 次询问，每次给定一个 $d$，保证 $S\cup\{d\}$ 与 $a$ 中元素均互不相同，求是否能将 $S\cup\{d\}$ 填入 $a$ 中 $0$ 的位置，使得 $a$ 与 $p$ 相似

$1\le n,q\le3\times10^5,0\le a_i\le10^6,1\le d,s_i\le10^6$

题解

Sol

套套套。

两个数组相似当且仅当其笛卡尔树相同。

注意到将一个集合能填到 $a$ 上，相当于我们求出每个节点子树里的最大值和祖先的最小值，得到一个区间 $[l_i,r_i]$，那么我们需要给集合中每一个数分配一个位置，使得 $S_i\in[l_i,r_i]$，未知节点之间的大小关系可以忽略，因为不难说明一定可以调整得到一个祖先均大于后代的树

也就是说我们现在得到了一些区间 $[l_i,r_i]$，要将 $S\cup\{d\}$ 每一个数对应一个区间，判断是否可行

根据 Hall 定理，不难发现我们需要检验的是对于任意区间 $[L,R]$，被其完全包含的 $[l_i,r_i]$ 个数小于其中 $S\cup\{d\}$ 元素个数，这个容易线段树扫一遍检验

但是 $d$ 不固定，我们可以先对 $S$ 扫一遍，然后看加入 $d$ 会产生哪些影响，具体地，如果我们线段树维护 $[L,R]-N([L,R])$（$[L,R]$ 为区间个数，$N([L,R])$ 为范围内数个数），那么影响相当于将所有经过 $d$ 的区间权值 $+1$

如果区间权值出现 $-2$ 显然无解，否则我们对每个 $R$ 找到最近的值为 $-1$ 的左端点 $ml_R$，那么最后的 $d$ 一定需要同时在所有 $ml_R$ 存在的 $[ml_R,R]$ 里，直接求出区间交判断即可

复杂度 $O(n\log n)$

17. CF1552H - Guess the Perimeter [K]

题面

交互题。

有一个矩形，满足其顶点均为整点且坐标在 $[1,200]$ 内，且其边界与坐标轴平行

你每次可以选择若干个整点，你会得到有多少个整点在矩形内（包含边界）

你可以询问 $4$ 次，你需要求出这个矩形的周长

题解

Sol

原神。

首先，将问题转化为在矩阵上的格子，产生的影响即将长宽分别 $-1$

这题看着没什么入手点，注意到我们可以先询问一下所有点然后得到矩形面积

这个问题和位置无关，那么我们需要找一个和位置无关的结构

经过一些尝试，我们发现可以询问所有偶数列，这样我们可以根据得到的答案是否是矩形面积的一半，判断出列数是否是偶数

扩展一下，我们询问所有模 $d$ 余 $0$ 的列，那么我们可以得到列数是否是 $d$ 的倍数

然后我就不会了。

editorial 说，我们可以首先二分出最大的 $2^k$ 使得列数是 $2^k$ 的倍数，由于我们只需要判断 $2^1\sim 2^7$ 内的数，因此需要 $3$ 次

不妨设询问 $d$ 得到的答案为 $f(d)$，那么行数即为 $|f(2^k)-2f(2^{k+1})|$，仔细一想这好像很有道理，因为询问 $2^k$ 的时候与该列相交的次数一定为奇数，而询问 $2^{k+1}$ 得到的一定是除以 $2$ 后两边的数

注意到二分出 $2^k$ 时一定已经求了 $f(2^{k+1})$（除了 $k=7$ 的情况，但这种情况 $f(2^{k+1})=0$，特判一下），因此最后就在 $4$ 次操作内解决了这个问题

18. CF1726G - A Certain Magical Party [S]

题面

有 $n$ 个人，每个人有一个开心度 $a_i$ 和一个属性 $b_i\in\{0,1\}$

你需要给这些人安排一个顺序，然后从左到右执行，对于当前的人 $i$：

如果 $b_i=0$，令 $x$ 表示剩下的人中 $a$ 值小于自己的数量，则 $a_i\leftarrow a_i+x$
如果 $b_i=1$，令 $x$ 表示剩下的人中 $a$ 值大于自己的数量，则 $a_i\leftarrow a_i+x$

求有多少顺序使得执行完之后所有人的 $a$ 值相等，对 $998244353$ 取模

$1\le n\le2\times10^5,1\le a_i\le2n$

题解

Sol

简单题。

这个操作很奇怪，所以我们先考虑一下有没有什么入手点

注意到所有人的开心度都是单增的，并且只会变化一次

观察 $a$ 最小的人，如果有一个 $b=0$ 的，那么只能是所有人都相等，直接判断是否满足，输出 $n!$ 或 $0$

否则，如果有 $\ge2$ 个 $b=1$ 的，那么这两个人最后的开心度一定不等，输出 $0$

那么只能恰有 $1$ 个 $b=1$ 的，而这个 $b=1$ 加完后的开心度一定为 $mn+n-1$，称其为 $aim$

如果有人 $>aim$，那么显然无解，判掉。

这启发我们从小到大考虑所有人，设当前的人为 $i$，共有 $c_0$ 个 $b=0$，$c_1$ 个 $b=1$：

对于 $b=0$ 的人，我们判一下前面的人数 $W$，那么如果 $i+W\ge aim$，因为 $i\le aim$，因此一定有恰好 $1$ 个位置可以插入到前面的序列使得最后加出来 $a$ 值是正确的，乘上 $c_0!$ 即可，否则无解
对于 $b=1$ 的人，需要分两种情况讨论：
- $i<aim$，那么此时如果有两个 $b=1$，根据前面的推理一定无解，输出 $0$，否则判断一下 $i+W+c_0\ge aim$，若成立这一个 $b=1$ 的人一定有恰好一个位置插入到前面，否则无解
- $i=aim$，那么这些人放在哪里都不会产生任何影响，乘上 $\binom n{c_1}c_1!$

复杂度 $O(n)$

19. CF1495F - Squares [E]

题面

有 $n$ 个点，给定 $1\sim n$ 的排列 $p_i$，按如下方式建有向图：

对每个 $i(1\le i\le n)$，向 $i+1$ 连一条权值为 $a_i$ 的边
对每个 $i(1\le i\le n)$，向右边第一个满足 $p_j>p_i$ 的 $j$ 连一条权值为 $b_i$ 的边，不存在则将边连向 $n+1$

$q$ 次询问，维护一个必经点 $S$，每次询问向 $S$ 中加入或删除一个点，查询 $1$ 到 $n+1$，且经过 $S$ 中所有点的最短路

$1\le n,q\le2\times10^5,|a_i|,|b_i|\le10^9$

题解

Flamire 做法

Sol

注意到这是一个三角剖分，那么我们补成三角剖分。

那么每个询问求的就是 $\sum dis(S_i,S_{i+1})$，差分一下就可以转化成 $O(q)$ 次对两点间距离的查询

考虑在三角剖分上分治，对于区间 $[l,r]$，设其分治点为 $m$，我们维护出 $l$ 到区间内每个点，区间内每个点到 $r$ 的距离，这个是容易用树状数组维护合并的

我们需要把查询挂到分治过程上：注意到对应的 $m$ 就是区间内分治深度最浅的点，这可以 st 表快速求出

每个区间就是查询一下 $dis(x,m)+dis(m,y)$ 即可

复杂度 $O(n\log n)$

题解做法

Sol

实际上，只要注意到这个图类似三角剖分的性质即可

我们倒着扫 $i$，维护 $i$ 到每个点的距离，设 $i$ 的 $b_i$ 边到的点是 $to_i$，那么 $(i,to_i]$ 的距离就是 $+a_i$，$(to_i,n+1]$ 的距离需要判断一下 $b_i$ 和 $dis_{to_i}+a_i$ 的大小，区间加上对应的值即可，可以直接树状数组维护

复杂度 $O(n\log n)$

20. CF1528F - AmShZ Farm [K] ✔️

题面

定义一个长为 $n$ 的数组 $a$ 是 more-equal 的当且仅当其每个元素都属于 $[1,n]$ 并且可以通过给每个元素加上一个非负整数使其变为一个 $1\sim n$ 的排列

对于一个长为 $n$ 的 more-equal 的数组 $a$ 和一个长为 $k$ 的数组 $b$，定义它们是 compatible 的当且仅当 $\forall b_i,1\le b_i\le n$，且 $a_{b_1}=a_{b_2}=\cdots,a_{b_k}$

给定 $n,k$，求有多少对 compatible 的序列，对 $998244353$ 取模

$1\le n\le10^9,1\le k\le10^5$

题解

Sol

考虑 more-equal 的限制，一个显然的判定条件是 $\le i$ 的元素个数要 $\ge i$，但这看起来就不是很能做。

考虑一个经典（？）的模型转化：依次考虑 $a_1,a_2,\cdots,a_n$，每次如果一个数在前面出现过，那么它就会往后走，走到第一个没有数出现的位置，然后加一个 $n+1$ 的节点接成环，那么一个序列 more-equal 当且仅当 $n+1$ 最后没有被占用

这时方案数已经很好算了，因为这个环上任意位置都是等价的，也就是说最后 $n+1$ 是空的概率是 $\frac1{n+1}$，那么方案数就是 $(n+1)^{n-1}$

考虑算上 $k$ 的贡献，由于所有数又是等价的，因此我们只用算一个数的贡献，再乘 $n+1$，而这个 $n+1$ 和概率的 $\frac1{n+1}$ 的贡献抵消了

对于一个数，我们枚举它用了多少次：

$\sum_{i=0}^n\binom nii^kn^{n-i}\\\sum_{i=0}^n\binom nin^{n-i}\sum_{j=0}^k\binom ij{k\brace j}j!\\\sum_{j=0}^k{k\brace j}j!\sum_{i=0}^n\binom ni\binom ijn^{n-i}\\\sum_{j=0}^k{k\brace j}j!\binom nj\sum_{i=j}^n\binom {n-j}{i-j}n^{n-i}\\\sum_{j=0}^k{k\brace j}j!\binom nj(n+1)^{n-j}$

考虑有如下事情：

$m^n=\sum_{i=0}^m\binom mi{n\brace i}i!\\$

使用二项式反演可以得到：

${n\brace m}m!=\sum_{i=0}^m(-1)^{m-i}\binom mii^n$

这个是可以卷积的，因此我们可以 $O(k\log k)$ 求出一行的第二类斯特林数，那么将其代入上面的式子就可以求出答案

复杂度 $O(k\log k)$

21. CF704E - Iron Man [E]

题面

一棵 $n$ 个点的树，上面有 $m$ 辆车，第 $i$ 辆车会在 $t_i$ 时刻在 $u_i$ 出现，向 $v_i$ 以一单位时间 $c_i$ 条边的速度行驶，运动是连续的

任意时刻如果两辆车处于同一位置它们就会爆炸，求最早一次爆炸的时间，或报告不存在

$1\le n,m\le10^5,0\le t_i\le10^4,1\le c_i\le10^4$

题解

Sol

先考虑链的怎么做，我们可以将问题改写为：给定 $m$ 条二维平面上的线段，一维是时间，一维是位置，求时间维度上最小的交点

这个问题我们可以对时间维扫描线，注意到如果没有交点，那么线段之间的位置大小是不变的，也就是说最小的交点一定出在位置大小相邻的车之间，插入的时候直接判一下即可

如果找到了这个交点，就可以直接在扫描到这个时刻时推出，这样一直都不会出现位置大小相对关系改变的情况，因此可以直接用 set 维护

对于树上的情况，我们可以把每一条重链拎出来当成一次链上的问题

复杂度 $O(n\log^2n)$

22. CF1696G - Fishingprince Plays With Array Again [E]

题解

定义一个数列的 $f(a)$ 如下：

你可以在一段连续 $t(t\in R^+)$ 时间内，执行如下一种操作：

选择 $1\le i<n$，$a_i\leftarrow a_i-xt$，$a_{i+1}\leftarrow a_{i+1}-yt$
选择 $1\le i<n$，$a_i\leftarrow a_i-yt$，$a_{i+1}\leftarrow a_{i+1}-xt$

其中 $x,y$ 为给定常数

$f(a)$ 为让 $a$ 中元素全部 $\le0$ 的最小时间

给定 $a_1,a_2,\cdots,a_n$，$q$ 次操作，每次单点修改，或者查询一个区间的 $f$

$2\le n\le2\times10^5,1\le q\le2\times10^5$

题面

Flamire 做法

here

题解做法

Sol

不妨设 $X\le Y$

考虑将原题写成一个线性规划的形式，令变量 $a_i,b_i$ 分别表示 $i,i+1$ 操作了多少次 $X,Y/Y,X$

那么这个问题可以写成：

$\text{minimize}\sum a_i+b_i\\Xa_1+Yb_1\le A_1\\Ya_{i-1}+Xa_{i-1}+Xa_i+Ya_i\le A_i\\Ya_{n-1}+Xa_{n-1}\le A_n\\a_i,b_i\ge0$

对偶：

$\text{maximize}\sum A_ix_i\\Xx_{i-1}+Yx_i\le1\\Yx_{i-1}+Xx_i\le1\\x_i\ge0$

神说，对偶之后的线性规划，存在一个最优解满足每个变量取值只有可能是 $0,\frac 1Y,\frac1{X+Y}$

神说，考虑最优解，一定是超空间里限制形成的凸包的某个端点，也就是说相当于我们选了一个子集的限制，让它们取等，唯一确定了一组合法 $x$ 的解

如果我们将一个涉及两个 $x_p,x_q$ 的取等限制看成 $p$ 到 $q$ 的一条边，$x_i\ge 0$ 的取等限制看成 $i$ 到 $i$ 的自环，那么最后确定出来的每个连通块至少有一个环，而由于我们只有 $i-i$ 与 $i-(i+1)$ 的边，因此环长度为 $2$ 或 $1$，环长为 $2$ 时这个连通块一定都为 $\frac1{X+Y}$，环长为 $1$ 时这个连通块都为 $0$ 或 $\frac1Y$（$\frac1X$ 太大了，会违反限制）

那么直接 $dp_{i,0/1/2}$ 表示 $x_i$ 的取值即可，线段树维护矩乘容易做到 $O(n\log n)$

23. CF1083F - The Fair Nut and Amusing Xor [S]

题面

给定 $n,k$，以及长为 $n$ 的数列 $a,b$，定义 $f(a,b)$ 为：每次将 $a$ 中一个长为 $k$ 的子段异或上 $x$，让 $a$ 变为 $b$ 的最小操作次数，不可能则为 $-1$

$q$ 次询问，每次单点修改 $a$ 或 $b$ 中的一个值，求 $f(a,b)$

$1\le k\le n\le2\times10^5,0\le q\le2\times10^5,0\le a_i,b_i<2^{14}$

题解

Sol

首先 $a$ 和 $b$ 可以异或起来得到 $c$，其次 $c$ 可以做差分，这样每次操作相当于同时给 $c_i$ 和 $c_{i+k}$ 异或上一个数

那么把序列按 $k$ 分组，每一组可以给相邻两个数异或上同一个数，那么也就是判断每一组内有多少前缀和为 $0$ 的位置

单点修改一个位置的值相当于给某两个序列的后缀异或上一个值，然后查询全局 $0$ 的个数

容易分块维护，存一下每块内每种数出现了多少，打一个异或标记即可

复杂度 $O(n\sqrt n)$

24. WC2024 - 线段树 [K] ⭐

题面

规定线段树上每个节点两个儿子的分界点，可以唯一确定一棵线段树

按照这种方式给出一棵 $[0,n)$ 的线段树，那么这棵线段树有 $2n-1$ 个节点

给定 $m$ 个区间 $[L_i,R_i]$，求有多少线段树节点的子集 $S$ 满足知道了 $S$ 中每个节点代表的区间的和，能够推出所有 $[L_i,R_i]$ 的和

对 $998244353$ 取模

$2\le n\le2\times10^5,1\le m\le2\times10^5$

题解

Sol

深刻感受到了自己的弱小。

感觉这个题，就是一些奇妙或者不奇妙的 trick 组合在一起。

首先，这个推出和可以看成是在两个前缀和之间连了一条边，我们最后要求 $m$ 对点是联通的

不难发现这是一个三角剖分，三角剖分上是可以 dp 的（其实就是在原来的线段树上 dp）

注意到对于当前区间 $[l,r)$，与 $l$ 联通的连通块和与 $r$ 联通的连通块在下标范围上一定是不交的，也就是说一段前缀属于 $l$，一段后缀属于 $r$（这中间可能有些点与 $l,r$ 均不联通）

我们对这个设 dp 状态，令 $f_{x,i}$ 表示 $l$ 与 $r$ 不联通，$l$ 所属连通块最大下标为 $i$ 的方案数，$g_x$ 表示 $l$ 与 $r$ 联通的方案数，那么我们首先考虑两边合并：

$f_{x,i}\leftarrow f_{lc,i}\times f_{rc,j}[i+1\ \text{与}\ j\ \text{之间的点不向外连}]\\f_{x,i}\leftarrow f_{lc,i}\times g_{rc}\\f_{x,i}\leftarrow g_{lc}\times f_{rc,i}\\g_x\leftarrow g_{lc}\times g_{rc}\\$

最后再决策一下 $l$ 到 $r$ 的边是否选择：

$g_x\leftarrow g_x+f_{x,i}$

这里最麻烦的是 $i+1$ 和 $j$ 之间的点不向外连的限制，这里我们可以使用 xor-hashing 解决，即给每个 $V_{L_i},V_{R_i}$ 异或上同一个随机值，然后对 $V$ 求前缀和，这样 $i+1$ 与 $j$ 之间不向外连当且仅当 $V_i=V_j$

那么我们得到了一个 $O(n^2)$ 的做法，考虑如何优化

我们观察这个转移形式非常优美，我们可以考虑把 $V$ 放到下标后重写一下转移（即 $f_{x,v}$ 表示所有 $V_i=v$ 的状态和）：

$f_{x,i}\leftarrow f_{lc,i}\times f_{rc,i}\\f_{x,i}\leftarrow f_{lc,i}\times g_{rc}\\f_{x,i}\leftarrow g_{lc}\times f_{rc,i}\\$

这个就可以直接线段树合并优化了，复杂度 $O(n\log n)$

25. SNOI2024 - 平方数 [E]

题面

给定 $a_1,a_2,\cdots,a_n$，求有多少 $[l,r]$ 满足 $\prod_{i=l}^ra_i$ 是平方数，并输出字典序前 $10^5$ 小的 $[l,r]$

$1\le n\le3\times10^5,1\le a_i\le10^{36}$

题解

Sol

魔怔。

这题看起来不是很正常，所以考虑不正常的做法

直接质因数分解肯定不太行，因此我们考虑一些非确定性做法

考虑平方数在任何模意义下一定都是二次剩余，那么我们可以随机 $T=60$ 个不为任意 $a_i$ 因数的质数，然后求前缀积的 $(p-1)/2$ 次方，那么一个 $[l,r]$ 是平方数的必要条件是 $l-1$ 和 $r$ 的前缀积在所有模数下 $(p-1)/2$ 次方都相同

直接判一下即可，复杂度 $O(Tn\log a)$

但实际上这个会 T，并且还有人卡了 $\le10^6$ 质数的判断，那怎么办。

从 $5\times10^6$ 之后开始搜 $60$ 个质数即可。

都到这时候了谁还关心正确性啊。

26. SNOI2024 - 公交线路 [E] ⭐

题面

给定一棵 $n$ 个点的树，点之间能连出 $\frac12n(n-1)$ 条路径，求有多少路径的子集 $S$ 满足：

对于两点 $u,v$，如果存在路径 $P\in S$ 使得 $u,v\in P$，那么 $u$ 和 $v$ 可以互相一步到达
$S$ 满足条件当且仅当任意两点间最多 $2$ 步可达

对 $998244353$ 取模

$1\le n\le3000$

题解

Sol

设 $u$ 能一步到达的点的集合为 $R_u$，那么不难发现 $R_u$ 是一个树上的连通块，题目要求的就是 $R$ 两两有交，这等价于所有 $R$ 都有交，也就是说至少有一个点的 $R$ 是全集

也就是说我们需要求有至少一个点的 $R$ 是全集的 $S$ 的数量

$R$ 是全集的点是一个连通块，因此我们可以使用点减边容斥，考虑如何求一个点 $u$ 的 $R_u$ 是全集的方案数

直接做不好做，我们考虑对每个叶子是否属于 $R_u$ 进行容斥，而一个子树内的叶子情况是类似的，我们可以如下简化：

对于第 $i$ 棵子树，子树大小为 $s_i$，叶子个数为 $a_i$，我们钦定其中 $x_i$ 个数不在 $R_u$ 中，那么这种钦定对答案的贡献就是：

$(-1)^{\sum x_i}\times 2^{\sum(n-s_i)x_i+\frac12((\sum x_i)^2-\sum x_i^2)}$

这个式子可以写成卷积的形式，边的处理是类似的，直接卷是 $O(n^2\log n)$ 的

然后我就被卡常了。

实际上对于父亲的子树，可以不容斥直接计算每个叶子都必须可达的方案数（相当于每个叶子会乘上 $2^{n-s_i-\sum x_i}-1$），这样复杂度就是树形背包的 $O(n^2)$ 了

27. SNOI2024 - 拉丁方 [K]

题面

对于一个 $n\times n$ 的矩阵，定义其为拉丁方当且仅当每行每列都是 $1\sim n$ 的排列

现给定一个 $n\times n$ 矩阵的左上角 $R\times C$ 子矩阵的元素，请你补全剩下的元素，使其为一个拉丁方

给出构造或判断无解

$1\le R,C\le n\le500$

题解

Sol

这个看起来就像是二分图相关的什么东西，但我不会建模。

实际上，如果我们要求描述一个 $n$ 阶拉丁方的限制，我们可以这样建模：

建立一个二分图，左部为行，右部为颜色，在行和列之间两两连边，我们需要做的就是将这个二分图拆成列数个完美匹配

这个是二分图边染色问题，我们可以一个二分图拆成最大度数个匹配

但是这个不能直接套到这题上来，因为我们一直信息是一个左上角，形状有点怪

有一个部分分是 $C=n$，先考虑这个怎么做，可以改一下上面的建模：

建立一个二分图，左部为列，右部为颜色，如果某列可以填某个颜色，那么在它们之间连边，我们需要做的就是将这个二分图拆成 $n-R$ 个匹配，分别填到每行

这个可以直接用二分图边染色，由于度数最大值为 $n-R$，所以也是一定有解的

那么对于 $C\neq n$ 的情况，考虑将其补成 $C=n$ 的情况，继续使用上面的建模：

建立一个二分图，左部为行，右部为颜色，如果某行可以填某个颜色，那么在它们之间连边，我们需要做的就是将这个二分图拆成 $n-C$ 个匹配，分别填到每行

注意到这里可能出现无解的情况，但是无解一定能够说明原题无解（上面 $R$ 行已经填不了了），如果有解，那么我们使用 $C=n$ 的情况一定能构造出解，因此我们任意取一组解即可

复杂度 $O(n^3)$

notes：二分图边染色

给定一个二分图，要求用最小的颜色数给每条边染色，使得不存在两个有公共点的边的颜色相同

这个问题的答案是最大度数，最大度数显然是下界，对于上界，我们可以给出构造性证明：

增量构造，每次加一条边 $(x,y)$，设 $x,y$ 所有邻边颜色的 $\text{mex}$ 分别为 $l_x,l_y$：

如果 $l_x=l_y$，那么直接将 $(x,y)$ 染成 $l_x$
否则不妨设 $l_x<l_y$，我们希望将这条边染成 $l_x$，为了做到这件事情我们需要进行一些调整，具体地，我们从 $y$ 开始，走一条颜色为 $l_x,l_y,l_x,\cdots$ 交替的增广路，由于 $x$ 没有 $l_x$ 的边，因此 $x$ 一定不会被这条增广路经过，我们把这条增广路上的所有边颜色 $l_x\rightarrow l_y,l_y\rightarrow l_x$，这样调整后一定可以将 $(x,y)$ 染为 $l_x$

不难发现上述构造过程中颜色一定不超过最大度数，复杂度是 $O(mn)$ 的

notes：$k$-正则二分图

注意到 $k$-正则二分图一定是满足 Hall 定理的，也即其有一个完美匹配

对于 $k$-正则二分图，我们可以通过每次删掉一个完美匹配，规约到更小规模的问题，从而构造一个二分图边染色

但是直接用 Dinic 做是 $O(km\sqrt n)$ 的（$m=kn$），复杂度不够优秀。

考虑优化求完美匹配的过程：

对于 $k=2^d$ 的情况

每次找一个欧拉回路，把左到右的边和右到左的边拆成两个图，选择其中一个图递归解决

复杂度 $2^dn+2^{d-1}n+\cdots+n=O(2^dn)=O(m)$

对于 $k$ 任意的情况

考虑一个神秘算法：

重复 $n$ 次，每次找到左边一个未匹配点，然后开始沿增广路随机游走（即左到右走非匹配边，右到左走匹配边），直到走到左边一个匹配点

将走出来的路径上的环全砍掉，然后把这条增广路上的所有边状态翻转

可以证明，当两边各剩下 $T$ 个点未匹配时，期望步数是 $O(\frac nT)$ 的，也就是说整体复杂度是 $O(n\log n)$ 的

28. USACO24FEB - Minimum Sum of Maximum [K] ✔️

题面

给定 $a_1,a_2,\cdots,a_n$，其中有 $k$ 个元素被钉住了

你可以随意交换没有被钉住的元素的顺序，求 $\sum_{i=1}^{n-1}\max(a_i,a_{i+1})$ 的最小值

$2\le n\le300,0\le k\le6$

题解

Sol

神仙题。

可以在两端加入两个 $10^6$，当作被钉住的元素，那么考虑两个被钉住的元素之间的其他元素怎么排，不妨设这两个被钉住的元素分别为 $v$ 和 $w$，且 $v\le w$

可以讨论一下这里面的元素是否有 $>w$ 和 $<v$ 的值，或者直接观察到将元素按 $v$ 到 $w$ 的方向升序排序就是最优的

那么容易证明，设段内（不包含 $v,w$）最大值为 $mx$，最小值为 $mn$，那么该段的贡献为所有数的和，额外加上 $\max(0,mx-w)-\min(mn,v)$，提一下常量，相当于我们需要最小化所有段的 $\max(mx,w)-\min(mn,v)$ 之和

然后我开始想指数级做法了，并不会。

考虑继续观察性质，如果两段的 $[mn,mx]$ 相交不包含，不妨设其满足 $mn_i<mn_j<mx_i<mx_j$，那么我们将 $i$ 中最大的元素与 $j$ 中最小的元素交换，一定会使两段区间都变为原来的子区间，这显然是不劣的

也就是说，所有段的 $[mn,mx]$ 包含或相离。

看题解看到这，还是不会。

我们将所有没有被钉住的权值排序，称为 $c$

考虑对这个区间树进行 dp，令 $dp_{l,r,S}$ 表示 $S$ 包含了若干棵兄弟子树的区间，且这些兄弟子树都在 $[l,r]$ 内

有三种转移：

$l$ 或 $r$ 没有用在 $S$ 中的区间上（也即用在了 $S$ 的祖先上），从 $dp_{l+1,r,S}$ 和 $dp_{l,r-1,S}$ 转移
$S$ 是一整棵子树，且 $l$ 和 $r$ 都用上了，那么我们选择一个区间 $i$ 作为根，从 $dp_{l+1,r-1,S-\{i\}}+\max(c_r,w_i)-\min(c_l,v_i)$ 转移
$S$ 是若干棵子树，且 $l$ 和 $r$ 都用上了，从任意一个位置将其裂成两部分，每部分都是若干完整的子树：枚举一个 $T\subset S(T\neq\varnothing)$，从 $dp_{l,m,T}+dp_{m+1,r,S-T}$ 转移过来，看起来我们还要枚举一个 $m$，这样复杂度就带 $n^3$ 了，不过实际上可以发现，如果 $[l,m]$ 内部还有不用在 $T$ 上的节点，那么我们把 $[l,m]$ 缩短一定不劣，也就是说 $m$ 取 $l+siz_T-1$ 是最优的，其中 $siz_T$ 是 $T$ 中所有段容量之和

转移即可，复杂度 $O(3^kn^2)$

29. USACO24FEB - Infinite Adventure [K] ⭐

题面

有 $n$ 个点，每个点有一个周期 $T_i$，保证 $T_i$ 是 $2$ 的幂，每个点有且仅有一条出边，第 $x$ 秒时，第 $i$ 个点的出边指向 $c_{i,x\bmod T_i}$

$q$ 次询问，每次给定三个整数 $v,t,\Delta$，问第 $t$ 秒从 $v$ 出发，每一秒走一条出边，走 $\Delta$ 次，最后会走到哪里

$1\le n\le10^5,1\le q\le5\times10^4,\sum T_i\le10^5,1\le t,\Delta\le10^{18}$

题解

Sol

火大了。

这个题看起来就是倍增，但是需要考虑怎么倍增。

我们发现，我们如果知道 $ t\bmod2^k$ 的模数，我们就可以一直处理直到某个点 $p$ 满足 $T_p>2^k$

因此我们考虑按如下方式设倍增数组：$g_{i,t}$ 表示从 $i$ 出发，时间模 $T_i$ 余 $t$，走到第一个 $T_j>T_i$ 的时间/位置，$f_{i,t,o}$ 表示从 $i$ 点出发，时间模 $T_i$ 余 $t$，走 $2^o$ 步会走到哪里，并且只有 $2^o<g_{i,t}$ 的 $f_{i,t,o}$ 有定义

用这个我们可以求出任意一个点向后走 $\Delta$ 步的结果，具体地：

如果当前走 $g$ 仍然在 $\Delta$ 步以内，那么我们就走一步 $g$，否则找到不超过 $\Delta$ 步的最大的 $f$，然后走一步 $f$

分析一下这样做的复杂度：每走一步 $f$ 会让我们的 $\Delta$ 减半，走完 $f$ 之后的 $T_i$ 是不确定的，而每走一步 $g$ 会让 $T_i$ 至少变大 $1$，而 $T$ 的最大值为 $O(\log n)$，因此我们求一次的复杂度是 $O(\log n\log V)$ 的

用这个预处理倍增数组+处理询问，复杂度是 $O(n\log n\log^2V+q\log n\log V)$ 的，无法通过

这个做法的缺陷在于没有利用到 $f$ 是倍增数组的性质，具体地，走完 $f$ 之后的 $T_i$ 可能变小，这样我们无法快速求出右半部分的答案，这导致了我们的复杂度是三个 $\log$ 的，因此我们考虑重设一下 $f$ 的状态使其 $T_i$ 不变小

我们令 $f_{i,t,o}$ 表示从 $i$ 出发，时间模 $T_i$ 余 $t$，走到第 $2^o$ 个 $T_j=T_i$ 的时间/位置，这样倍增的时候就容易常数时间推出下一层

现在考虑如何利用 $f$ 求答案：

如果当前走 $g$ 仍然在 $\Delta$ 步内，那么就走一步 $g$，否则一直走 $f$，然后走一步原来的边

这样的复杂度：$g$ 每走一次，能达到的最大 $T$ 就至少减 $1$，而每一个 $T$ 我们最多会走 $\log V$ 次 $f$，因此求一次的复杂度依然是 $O(\log n\log V)$ 的

接下来的问题是怎么求 $f_{i,t,0}$，这个我们先从 $i$ 走一步，然后不断跳 $g$ 即可，这样复杂度是 $O(\log n)$ 的，可能需要把所有点按照 $T_i$ 大小排序后处理

那么最后的复杂度就是 $O(n\log V+q\log n\log V)$