task2

我突然想新开一个了/cy

[TOC]

1. CF1605F - PalindORme [Keter] ✨

题面

定义一个序列 $a_1,a_2,\cdots,a_n$ 是好的当且仅当你可以重排它，使得对于任意一个 $i$，它长为 $i$ 的前缀按位或和长为 $i$ 的后缀按位或相等，求有多少长度为 $n$，值域为 $[0,2^k)$ 的序列是好的，对大质数 $m$ 取模

$1\le n,k\le80,10^8<m<10^9$

题解

[Sol]

考虑如何判断一个序列是否是好的序列，我们可以由外向里构造，每次删掉一对相等的数 $x$，然后对于每个数，将 $x$ 中为 1 的位直接从中删去，重复这一过程，那么最后好序列删完之后至多剩一个，这样是正确的，因为一对数相等之后，不管怎么操作，它们一定继续相等

神说，你可以在坏序列上也跑这个过程，跑的过程中删除的子序列组成了一个好序列，你可以通过这个建立一个坏序列到规模更小的好序列的映射，每个坏序列都可以映射到一个规模更小的好序列，而剩下的部分的方案数你可以算，这样你就可以通过规模更小的好序列个数推出坏序列个数，也就推出了当前的好序列个数

但是如果直接跑这个会出现问题，如果最后删出来了奇数个相等的数，那么最后一定会剩下一个，这样坏序列对应的好序列不唯一，无法计数。

因此，我们定义一个“合法好序列”，合法好序列要求我们按照上述过程删完后删空或者只剩一个 $0$，这样不难发现，我们按照上述过程删除，最后如果有 $0$ 就将它也一并删除，那么删除的数一定组成一个合法好序列，并且每个非合法好序列都对应恰好一个合法好序列

那么我们就可以 dp 了

令 $all_{i,j}$ 表示长为 $i$，恰好包含 $j$ 个二进制位的序列个数

令 $h_{i,j}$ 表示长为 $i$，恰好包含 $j$ 个二进制位的，元素非零且互不相同的序列个数（非合法好序列删完合法好序列后剩下的部分）

令 $g_{i,j}$ 表示长为 $i$，恰好包含 $j$ 个二进制位的非合法好序列个数

我们有：

$$all_{i,j}=\sum_{x=0}^j(2^x)^i(-1)^{j-x}\binom jx\\h_{i,j}=\sum_{x=0}^j(-1)^{j-x}\binom jx(2^x-1)^{\underline i}\\g_{i,j}=\sum_{a=0}^{b-1}\sum_{b=0}^{j-1}\binom ia\binom jbh_{i-a,j-b}(all_{a,b}-g_{a,b})(2^b)^{i-a}$$

注意这里 $g$ 求的是非合法序列个数，因此最后要减掉不是合法序列但是好序列的个数（也就是当 $n$ 为奇数的时候 ban 掉 $i=n,a=n-1$ 的转移）

复杂度 $O(n^4)$

---

2. CF1179D - Fedor Runs for President [Euclid] ✔️(✨)

题面

给定一棵 $n$ 个点的树，求加一条边之后这棵树上最多有多少长度 $\ge2$ 的简单路径

$2\le n\le5\times10^5$

题解

[做法 1]

考虑如果我们连了 $(u,v)$ 这条边，设 $(u,v)$ 在原树中路径上的点分别为 $p_1,p_2,\cdots,p_k$，那么连接这条边之后会多出 $\sum_{i\neq j}siz_{p_i}siz_{p_j}$，而推一下就可以发现我们只要使 $\sum siz_{p_i}^2$ 最小即可

那么我们考虑 dp，令 $dp_i$ 表示 $i$ 子树内链上的 $siz^2$ 和最小值，转移是容易的，考虑如何统计答案

一条路径 $(u,v)$ 的答案，我们可以在 lca 处统计，也就是说我们对每个点求 $\min(dp_{v_1}+dp_{v_2}+(n-siz_{v_1}-siz_{v_2})^2)$

我们发现枚举 $v_1$ 之后这个式子是一个斜率优化的形式，直接按照 $siz$ 排序即可，复杂度 $O(n\log n)$

[做法 2]

考虑刚才合并的过程，我们的式子是 $\min(dp_{v_1}+dp_{v_2}+(n-siz_{v_1}-siz_{v_2})^2)$

那么不难发现，对于 $siz$ 相等的两个儿子，只有 dp 值最大的有用

因此我们考虑用 $O(\sum \text{儿子 siz 种数}^2)$ 的复杂度解决这个问题，我们可以证明，这样总复杂度是 $O(n\log\log n)$ 的：

我们令 $f(n)$ 表示 $n$ 个节点时的最坏复杂度

我们假设一些事情：$f(a+b)\ge f(a)+f(b)$，$f(a+1)-f(a)\ge f(a)-f(a-1)$

那么如果我们设根节点 $siz=i$ 的儿子有 $a_i$ 个，有 $f(n)=h^2+\sum a_if(a_i)$，其中 $h$ 是不同 $siz$ 个数

引理 1：对于使得 $f(n)$ 最大的树，根节点的 $a_i$ 满足对于任意 $i$，$a_i\le1$

证明：如果我们有一个位置 $i$ 满足 $a_i\ge2$，那么我们找到最大的 $m$ 使 $a_m\ge1$，那么我们进行 $a_i\leftarrow a_i-1$，$a_m\leftarrow a_m-1$，$a_{i+m}\leftarrow a_{i+m}+1$，由于 $h$ 不变且 $f(i+m)\ge f(i)+f(m)$，所以这样调整一定不会更劣

引理 2：对于 $f(n)$ 最大的树，子树大小一定是 $1,2,\cdots,k,n-\frac12k(k+1)$，且 $n-\frac12k(k+1)>k$

证明：考虑由于 $f(a+1)-f(a)\ge f(a)-f(a-1)$，那么就有对于 $x\le y$，$f(y+1)-f(y)\ge f(x)-f(x-1)$，也就是 $f(x)+f(y)\le f(x-1)+f(y+1)$，因此，如果我们有两个位置 $x,y(x\le y)$ 使得 $a_{x-1}$ 为 0，$a_x$ 为 1，$a_y$ 为 1，$a_{y+1}$ 为 0，我们就可以将 $a_x$ 和 $a_y$ 上的 1 调整到 $a_{x-1}$ 和 $a_{y-1}$ 上

那么我们考虑对这个树进行重链剖分，重儿子一定是 $n-\frac12k(k+1)$

在一条重链上，我们每向下走一步的 $h$ 是 $O(k)$，会花费 $O(k^2)$ 的代价，而子树大小也减小了 $k^2$，因此处理一条重链的复杂度是 $O(\text{子树大小})$

考虑一个点对多少条重链产生贡献，一个轻儿子向上跳一条轻边一定会至少使子树大小平方，因此一个点最多向上跳 $O(\log\log n)$ 次，每个点最多产生 $O(\log\log n)$ 的贡献，所以整体复杂度为 $O(n\log\log n)$

[做法 3]

进行一些猜测。

我们模仿直径求法，选择任意一个端点 $s$，找到连接 $(s,u)$ 后答案最大的 $u$，然后找到连接 $(u,v)$ 后答案最大的 $v$，$(u,v)$ 就是最优解

证明的话考虑这样一张图：

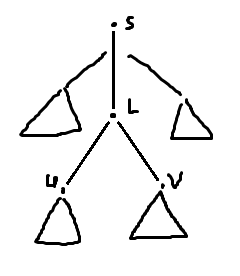
其中 $L$ 是 $\text{lca}(u,v)$，那么我们需要证明，对于所有若 $(u,s)$ 优于 $(v,s)$，则不存在一个 $(v,w)$ 使得其为最大值：

若 $w$ 在 $L$ 子树内，那么 $(u,v)$ 优于 $(v,w)$

若 $w$ 不在 $L$ 子树内，那么 $(u,w)$ 优于 $(v,w)$

因此，直接这样做就是对的，复杂度 $O(n)$

---

3. luoguP5361 - [SDOI2019] 热闹的聚会与尴尬的聚会 [Keter] ⭐

题面

$T$ 组数据，每次给定一张 $n$ 个点，$m$ 条边的无向图，构造两个点集 $P,Q$，定义 $p$ 为 $P$ 的导出子图上的点的度数最小值，$q$ 为 $|Q|$，要求 $Q$ 内的点互相没有边直接相连，且 $\left\lfloor\dfrac n{p+1}\right\rfloor\le q$ 且 $\left\lfloor\dfrac n{q+1}\right\rfloor\le p$

$1\le T\le32,1\le n\le10^4,1\le m\le10^5$

题解

[Sol]

$p$ 的最大值是好求的，每次删除度数最小的点，那么所有删除的点中度数最大值就是 $p$ 的最大值

考虑 $Q$ 如何构造，题目给的限制实际上是 $(p+1)(q+1)>n$

那么我们只要保证 $Q$ 中的点每次带走的点不超过 $p+1$ 个即可

而考虑我们求 $p$ 的最大值的过程，这之中每次我们删除的点度数一定 $\le p$，因此我们按这个顺序选择 $Q$ 中的点，每次找到一个未被标记的点就将它加入 $Q$，并且将相邻的点全部打上标记，这样每个 $Q$ 中的点最多带走 $p+1$ 个点，所以构造出来是符合条件的

复杂度 $O(n\log n)$

---

4. ARC158D - Equation [Euclid] ⭐

题面

$T$ 组数据，给定 $n,p$，求一对 $(x,y,z)$ 使得：

• $1\le x<y<z\le p-1$

• $(x+y+z)(x^n+y^n+z^n)(x^{2n}+y^{2n}+z^{2n})\equiv x^{3n}+y^{3n}+z^{3n}\pmod p$

$T\le10^5,1\le n\le10^9,5\le p\le10^9$，保证 $p$ 为质数

题解

[Sol]

$x<y<z$ 可以转化成互不相同，输出的时候再排序即可

由于 $p$ 为质数，所以有逆元，那么设 $x=az,y=bz$

第二个条件就是 $(a+b+1)(a^n+b^n+1)(a^{2n}+b^{2n}+1)z^{3n+1}\equiv (a^{3n}+b^{3n}+1)z^{3n}$

由于 $z\not\equiv0$，所以可以把 $z^{3n}$ 除掉，那么只要 $(a+b+1),(a^n+b^n+1),(a^{2n}+b^{2n}+1),(a^{3n}+b^{3n}+1)$ 非零，我们就可以通过一次逆元计算解出 $z$

那么我们在 $[2,p-1]$ 内随机选择 $a,b(a\neq b)$，直到上述四个式子均非零为止，毛估估一下次数不会很多

事实上，editorial 给了证明，对于任意 $i$，$(a^i+b^i+c^i)\equiv0\pmod p$ 的概率最多为 $\frac14$，但我懒得看了

复杂度 $O(T\log n)$

---

5. ARC158F - Random Radix Sort [Euclid] ✔️

题面

给定 $n,m,k$，以及一个长为 $n$ 的正整数数列 $a_1,a_2,\cdots,a_n$

每次你可以选择一个十进制位，以这一位为关键字进行稳定排序，你进行了这个操作 $m$ 次

现在再给定 $b_1,b_2,\cdots,b_n$，问对于所有 $k^m$ 种可能的操作序列，有多少能使 $a$ 变为 $b$

$1\le n\le2\times10^5,1\le m\le10^9,1\le k\le18,0\le a_i,b_i<10^k$

题解

[Sol]

缝。

考虑所有 $b$ 中相邻两个数之间的顺序关系，如果一个操作序列满足对于任意 $i$，经过这个操作序列后 $b_i$ 在 $b_{i+1}$ 之前，那么这个操作序列就是合法的

那么我们考虑 $b_i$ 在 $b_{i+1}$ 之前的充要条件是什么，我们可以倒着考虑，设 $b_i$ 比 $b_{i+1}$ 小的数位集合为 $A$，$b_i$ 比 $b_{i+1}$ 大的数位集合为 $B$，那么 $\text{last}(B)\ge\text{last}(A)$，其中 $\text{last}$ 表示集合内的位最后一次操作的位置，并且如果在原序列中 $b_i$ 在 $b_{i+1}$ 之后，则必须要有 $A$ 中元素出现至少一次

我们发现，现在限制都只跟每位的 $\text{last}$ 有关，而这之外的部分我们可以使用一些计数手段解决

考虑如下 dp：令 $dp_{S}$ 表示 $S$ 中的位 $\text{last}$ 的相对顺序种数，转移的时候我们枚举 $\text{last}$ 最大的位是哪个，然后判断一下是否会违反限制即可，这部分可以用高维前缀和做到 $O(2^kk)$

由于不同相对顺序以及位的集合本质相同，现在问题转化成：我们要计数长为 $m$，值域为 $[1,x]$，且 $\text{last}$ 的相对顺序关系是 $1,2,\cdots,x$ 的序列数量

考虑倒着做，每新出现一个 $\text{last}$，非 $\text{last}$ 的数的选择就会 $+1$，那么我们要计数的就是长为 $m-x$，值域为 $[1,x]$ 的递增序列的元素乘积之和，这个显然可以矩乘做到 $O(k^3\log m)$，由于我们要对每个 $x$ 做一次，复杂度是 $O(k^4\log m)$

那么最后复杂度就是 $O(nk+2^kk+k^4\log m)$

似乎 std 是 $O(nk+2^kk+k\log m)$ 的，不过反正瓶颈不在这里。

---

6. AGC059C - Guessing Permutation for as Long as Possible [Keter]

题面

有一个长为 $n$ 的排列 $p$，但你不知道它是什么

但你有一个长为 $\frac12n(n-1)$ 的无序二元组序列 $(a_i,b_i)$，每个无序二元组恰好出现一次

你会依次询问这个二元组序列，对二元组 $(a_i,b_i)$，你会询问 $p_{a_i}<p_{b_i}$ 是否为真，但是如果你能通过前面的询问推出当前询问的答案，你就不会问这个问题

求有多少排列会使得你问 $\frac12n(n-1)$ 次问题，对 $10^9+7$ 取模

$2\le n\le400$

题解

[Sol]

被诈骗了，愤怒。

考虑三个位置 $(a,b,c)$，不妨设出现最晚的是 $(b,c)$，这就会对 $p$ 产生一个 $[p_a<p_b]=[p_a<p_c]$ 的限制

我们直接对每对位置拆点，拆成 $p_a<p_b$ 的点和 $p_b<p_a$ 的点，对于每个 $(a,b,c)$，我们只需要用并查集 merge 一下即可

最后会形成若干个连通块，如果存在 $p_a<p_b$ 和 $p_b<p_a$ 在同一联通块，显然误无解，否则答案就是 $2^{\text{连通块个数}/2}$

复杂度 $O(n^3\alpha(n))$

---

7. AGC043D - Merge Triplets [Safe]

题面

问有多少长为 $3n$ 的排列能通过 $n$ 个长为 $3$ 的数组进行归并排序得出，对大质数 $m$ 取模

$1\le n\le2000,10^8\le m\le10^9+7$

题解

[Sol]

设排列为 $p$，$n$ 个数组分别为 $a_1,a_2,\cdots,a_m$

考虑最大值的位置，最大值一定在最后三个数中的一个，并且后面的数一定在 $a$ 中被堵在最大值后面的，我们将后面的数选出，并从 $p$ 和 $a$ 中删去

问题转化为，我们每次从 $p$ 中删去最后 $x(x\le3)$ 个数，然后选择一个长度 $\ge x$ 的 $a$ 数组，将它的长度 $-x$，要计数的就是不同的操作 $x$ 的方案数（再乘上选出 $x-1$ 个被堵住的数的方案数）

直接计算有可能会采用不同的选 $a$ 的方案而算重，因此我们想一想有没有充要条件，如果有 $A$ 个长为 $3$ 的数组，那么能删完当且仅当 $x=2$ 的数量小于等于 $x=1$ 的数量

那么我们就可以 dp 了，令 $dp_{i,j}$ 表示当前 $p$ 的长度为 $i$，$x=1$ 比 $x=2$ 多 $j$ 个，转移是容易的

复杂度 $O(n^2)$

---

8. ARC156F - Make Same Set [Keter] ✨

题面

给定三个长为 $n$ 的数列 $a,b,c$，构造一个元素数量最多的集合 $S$，使得它可以通过如下两种方式得出：

1. 一开始你有一个空集，对于每个 $i$，向这个集合中加入 $a_i$ 和 $b_i$ 中的一个
2. 一开始你有一个空集，对于每个 $i$，向这个集合中加入 $a_i$ 和 $c_i$ 中的一个

$1\le n\le5000,1\le a_i,b_i,c_i\le10000$

题解

[Sol]

考虑如果每次 $a_i$ 和 $b_i$ 可以不加入，$a_i$ 和 $c_i$ 也可以不加入，那么有一个网络流建模（图源 editorial）：

图中每条边流量都为 $1$，不难发现这样建模就是正确的

但是如果我们有一个 ai or bi 的点，使得 $a_i$ 和 $b_i$ 都没有流过，那么这个点相当于什么都没有选，我们需要避免这种情况，对于 ai or ci 同理，称这样的点是坏点

我们可以证明，如果我们一直按照最短的增广路增广，一定不会出现新的坏点

具体地，如果我们走了一条增广路后出现了新的坏点，那么我们可以证明一定存在更短的增广路

如图， a5 or b5 是多出来的坏点，那么 a5 or b5 连向的两个点一定是没有流过的，因此 a5 or b5 连出的两条边都没有流过，S 连向 a5 or b5 的边也就没有流过，因此可以按如上的方式调整获得一个更短的增广路

那么我们只要保证一开始没有坏点，直接跑 dinic 就可以了

而最开始全流 $a_i$ 就是一个没有坏点的方案，那么我们建图的时候模拟这样流完的过程即可

复杂度 $O(n\sqrt n)$

---

9. ARC148E - ≥ K [Keter] ⭐

题面

给定 $a_1,a_2,\cdots,a_n$，求有多少 $a$ 的重排使得任意两个相邻数的和都 $\ge k$，对 $998244353$ 取模

重排相同当且仅当每一位的元素值相同

$2\le n\le2\times10^5,0\le k,a_i\le10^9$

题解

[Sol]

考虑将 $a$ 从小到大排序，考察 $a_1+a_n$ 与 $k$ 的大小关系，如果 $\ge k$，说明 $a_n$ 可以和任何数相邻，如果 $<k$，说明 $a_1$ 不能和任何数相邻，这启发我们按照某种顺序考虑这个问题，使得每个 $a_i$ 要么不能和后面的任何一个数相邻，要么可以和后面的任何一个数相邻，这样就方便计数了

有了这个之后就是好计数的，假设初始我们有 $1$ 个空位，我们将 $a$ 从小到大排序，如果当前还没有考虑的下标范围是 $[l,r]$，那么我们比较 $a_l+a_r$ 和 $k$ 的大小关系：

• 若 $a_l+a_r\ge k$，那么 $a_r$ 可以和任何数相邻， 将 $a_r$ 插入任意一个空位，这步操作后会使空位数 $+1$
• 若 $a_l+a_r<k$，那么 $a_l$ 不能和后面任何数相邻，将 $a_l$ 插入任意一个空位，这步操作后会 ban 掉它相邻的两个空位，也就是使空位数 $-1$

显然，答案就是过程中空位数的乘积

最后需要除掉相同数个数的阶乘

复杂度 $O(n\log n)$

---

10. AGC007E - Shik and Travel [Keter] ⭐

题面

给定一棵 $n$ 个点的以 $1$ 为根的树，边有边权，这棵树每个点要么为叶子，要么有恰好两个儿子

你需要对这棵树进行 dfs，假设你访问叶子的顺序为 $lf_1,lf_2,\cdots,lf_k$，你需要最小化 $\max(dis(lf_i,lf_{i+1}))$，求这个最小值

$2<n<131072$

题解

[Sol]

首先可以二分。

观察到走到第一个叶子和从最后一个叶子返回的代价不需要计算

考虑一个 dp，令 $dp_{u,l,r}$ 表示走完 $u$ 的子树，走到第一个叶子的距离为 $l$，从最后一个叶子走回来的距离为 $r$，是否可以满足全程 $\le mid$

一件显然的事情就是如果存在两个状态满足 $l_1\le l_2,r_1\le r_2$，那么 $(l_2,r_2)$ 一定没有意义

因此，我们对每个节点维护的一定是若干个 $l$ 递增，$r$ 递降的状态，我们不妨将它们按 $l$ 排序

考虑如何合并两棵子树 $lc,rc$，那么对于每个 $(lc,l_1,r_1)$，它能转移到的状态在按 $l$ 排序后一定是一段前缀，可以用 two-pointer 来做到 $O(\text{状态数})$ 合并

那么我们的整体复杂度就是 $O(\text{状态数})$ 的

你可能认为这样过不去。You’re wrong, here’s why.

一个点的有效状态的上界是 $2\min(siz_{lc},siz_{rc})$，所以总状态数是 $O(n\log n)$ 的

那么总复杂度就是 $O(n\log n\log w)$

---

11. AGC056B - Range Argmax [Euclid] ✔️

题面

给定 $n$，再给定 $m$ 个区间 $[l_i,r_i]$

对于所有 $1\sim n$ 的排列 $p$，我们构造长为 $m$ 的数列 $x_i$，其中 $x_i$ 为 $p[l_i:r_i]$ 中的最大值下标

求有多少不同的 $x$ 数列，定义不同当且仅当有一位值不同，对 $998244353$ 取模

$2\le n\le300$

题解

[Sol]

考虑用最大值将序列切开，那么对于经过这个最大值的区间，它们的 $x$ 都一定在最大值的位置，这样我们就可以将问题划分为两个独立的问题进行区间 dp

但是这样有可能算重，我们如果切了 $x$ 后切了 $y$，且不存在区间同时经过 $x$ 和 $y$，那么这和先切 $y$ 后切 $x$ 其实是一样的，这样就会算重

因此我们钦定，当处理所有在 $[l,r]$ 内的区间时，我们切的点 $x$ 一定满足所有经过 $x$ 的区间的最小 $l$ 端点 $l_\min$，下一步切的必须在 $[l_\min,x)$ 内，这样满足切点 $x$ 之前的位置和 $x$ 都不会等价

那么我们需要给 dp 状态加一维 $x$，表示切的位置必须在 $[x,r]$ 内，$l_\min$ 可以预处理做到 $O(1)$ 转移

复杂度 $O(n^3)$

---

12. AGC029F - Construction of a tree [Keter] ✨

题面

给定 $n$ 个点集 $E_1,E_2,\cdots,E_{n-1}$，构造一棵树，使得对于任意 $i$，其第 $i$ 条边 $(u_i,v_i)$ 满足 $u_i,v_i\in E_i$，或判断无解

$2\le n\le10^5,\sum|E_i|\le2\times10^5$

题解

[Sol]

魔法题。

首先，你观察到一个必要条件：对于任意一个 $\{E_1,E_2,\cdots,E_{n-1}\}$ 的子集 $S$，$S$ 中的集合的并 $f(S)$ 一定满足 $|f(S)|\ge|S|+1$，如果该条件不成立，那么 $S$ 中这些点集连出的边一定会成环，不符题目条件

这个条件长得很像霍尔定理，那么我们建出一张二分图，左部是点，右部是 $E_i$，如果 $u\in E_i$ 那么从 $u$ 向 $E_i$ 连边，而我们的必要条件就是要求任意一个右部集合连出去的点数都大于这个集合的大小，也就是说对于任意大小为 $n-1$ 的左部点集，我们一定能找到一个和右部点的完美匹配，因此，我们如果找不到大小为 $n-1$ 的匹配，说明无解

实际上，这个条件也是充分条件，这点可以构造证明：

如果对于任意 $S$ 有 $|f(S)|\ge|S|+1$，我们考虑这样的一个策略，先找出一个大小为 $n-1$ 的匹配，一定有一个左部点不在匹配内，设其为 $r$

我们从 $r$ 开始 bfs，每次新搜到一个相邻的没有被访问过的右部点，我们就将与其匹配的左部点加入队列，如果这个点为 $v$，那么我们就构造了一条树边 $(r,v)$

如果这个过程中，我们出现了找不到没有访问过的右部点的情况，那么设当前没有被访问过的右部点的集合为 $T$，则 $T$ 连出去的边一定都指向和 $T$ 匹配的点集中的某一个点，因此 $|f(T)|=|T|$，与我们的假设矛盾，所以如果满足 $|f(S)|\ge|S|+1$，一定可以通过上述方式构造出解

复杂度 $O(\sum|E_i|\sqrt n)$

---

13. luoguP8292 - [省选联考 2022] 卡牌 [Safe]

题面

给定 $s_1,s_2,\cdots,s_n$，有 $m$ 次询问，每次给定 $c_i$ 个质数 $p_{i,j}$，你需要输出有多少 $s$ 的子集使得元素乘积能被所有 $p_{i,j}$ 整除，对 $998244353$ 取模

$1\le n\le10^6,1\le s_i\le2000,1\le m\le1500,1\le c_i,\sum c_i\le18000,2\le p_{i,j}\le2000$

题解

[Sol]

rematch 了属于是。

首先，$n$ 显然没有什么用，我们可以直接用桶

考虑根号分治，$\ge43$ 的质因子一定不能乘在一起，因此我们可以按照每个数 $\ge43$ 的质因子进行分组，对于 $<43$ 的质因子，我们进行状压

那么每次询问相当于我们钦定一些组内必须选至少一个数，剩下组内可以一个都不选，要求最后选出来的数 $<43$ 的质因子或起来是某一个集合的超集

对每组，至少选一个数和可以不选都是可以用 fwt 预处理的，注意到我们不需要 fwt 回去，而一个数只有两个位置有值，所以这部分可以做到 $O(2^{13}V)$

我们预处理出所有组都可以不选的 fwt 点值，那么每次询问就是将一些可以不选的组改为必须选一个，由于点值显然都非零，可以直接除掉，可以在前面用线性求逆元预处理出来

得到每次询问的点值之后做一次 fwt 即可

复杂度 $O(2^{13}V+m2^{13}\cdot13+\sum c_i2^{13})$，似乎跑的很快

---

14. AGC022E - Median Replace [Euclid]

题面

我们每次可以对一个 01 串进行如下操作：

选择三个相邻的字符，将它们替换为它们的中位数，操作后序列长度减小 $2$

定义一个 01 串是好的，当且仅当它长度为奇数，且可以通过若干次操作后只剩一个 1

给定一个由 01? 组成的字符串 $s$，问有多少将 ? 替换为 0 或 1 的方式使得得到的串是好串，对 $10^9+7$ 取模

$1\le|s|\le3\times10^5$

题解

[Sol]

考虑好串的充要条件是什么。

一个显然的贪心是如果有 000 我们肯定会先把它删掉

我们可以假设有一个栈，从栈顶到栈底依次是一段 0 和一段 1

如果我们遇到一个 0：

• 栈顶有两个 0，将这两个 0 与当前的 0 一并消掉，然后插入一个 0
• 否则直接入栈

如果我们遇到一个 1：

• 栈顶为 1，这说明栈里只有 1，直接将这个 1 入栈
• 栈顶为 0，我们直接将这个 0 和当前的 1 消掉，这样看起来就很优

最后判断一下栈中 1 的个数是否大于 0 的个数即可，这看起来就很对

由于 0 的个数最多只有 $2$，所以我们 1 的个数也只用记四种状态即可，复杂度 $O(n)$

---

15. luoguP8907 - [USACO22DEC] Breakdown P [Keter] ⭐

题面

给定一张 $n$ 个点，$n^2$ 条边的有向完全图（有 $n$ 个自环）以及整数 $k$，边有边权

$n^2$ 次询问，每次删掉一条边，询问剩下的图从 $1$ 到 $n$ 恰好经过 $k$ 条边的最短路（可以重复经过点或边），如果无解输出 -1，询问之间不独立

$1\le n\le300,2\le k\le8$

题解

[Sol]

神秘。

考虑 $k$ 非常小，因此我们应该考虑指数级算法

首先不同状态只有 $O(n)$，因此我们可以考虑折半，每次询问的时候用 $O(n)$ 的时间合并，那么我们需要维护 $1$ 到每个点经过 $2,3,4$ 条边的最短路（对于 $n$ 同理）

把操作倒过来，变为每次加边 $u\rightarrow v$，我们需要更新一些最短路，一个显然的事情是我们更新的路径一定要经过 $u\rightarrow v$

这里只讨论从 $1$ 出发的情况，到 $n$ 的情况是对称的

我们考虑通过直接枚举路径上的点来更新答案

那么经过 $k$ 条边的路在 $u=1$ 和 $u\neq1$ 的情况下需要枚举的点数如下所示：

	$u=1$	$u\neq1$
$k=2$	1	0
$k=3$	2	1
$k=4$	3	2

这样 $k=4$ 时的复杂度为 $O(n^3\cdot n+n^2\cdot n^2)=O(n^4)$，所以我们寄了。

那我们考虑平衡一下复杂度，对于 $k=2$，我们对于任意两个点 $x,y$，都维护 $x$ 到 $y$ 经过恰好 $2$ 条边的最短路，这样在 $k$ 更大的时候我们就可以少枚举一个点

那么需要枚举的点数就变为了下表：

	$u=1$	$u\neq1$
$k=2$	1	1
$k=3$	1	1
$k=4$	2	1

这样复杂度就是 $O(n^3)$ 的了

---

16. luoguP8907 - [USACO22DEC] Making Friends P [Euclid]

题面

给定一张 $n$ 个点 $m$ 条边的无向图，每次删掉编号最小的点，并在这个点此时所有邻点之间两两连边（如果原来有边则不连），所有点删完后问总共加了多少条新边

$2\le n\le2\times10^5,1\le m\le10^5$

题解

[Sol]

考虑这张图会有很多团，那我们直接来维护这些团。

我们对每个团用一个 set 来维护，这张图一定是若干个团再加上一些边，且两个团可以有重复节点

那么每次删除一个点 $u$ 的时候，我们首先需要将包含这个点的团都合并起来，再加入所有此时不在团中的与 $u$ 直接相连的点

我们对它使用启发式合并，那么复杂度就是总点数 $\times\log^2$（一个 $\log$ 是启发式合并，另一个是 set）

而我们每个点在初始会被加入一次，之后最多被单独加入 度数 次，所以总点数是 $O(n+m)$ 的

那么总复杂度 $O((n+m)\log^2(n+m))$

---

17. luoguP8908 - [USACO22DEC] Palindromes P [Keter] ✔️

题面

给定一个只包含 G 和 H 的字符串 $s$，对 $s$ 的所有 $\frac12n(n+1)$ 个子串 $t$，你需要求出 $f(t)$ 之和，$f(t)$ 定义如下：

对于一个字符串 $t$，最少交换多少次相邻字符，才能使 $t$ 变为回文串，如果不可能则 $f(t)=-1$

$1\le n\le7500$

题解

[Sol]

首先考虑怎么求一个字符串的 $f$ 值

判无解是容易的，无解当且仅当长度为偶数并且 G 的个数为奇数

交换两个相同字符一定是无意义的，因此所有 G 的相对位置关系都不变

这意味着在回文串中，一定是第 $i$ 个 G 和倒数第 $i$ 个 G 配对

那么我们考虑枚举中间的两个 G（如果奇数个 G 的话就枚举中间一个），这样之后我们遇到的所有 G 匹配关系都确定了

设我们枚举的两个 G 下标为 $x,y(x<y)$，$x$ 前面第 $i$ 个 G 是 $u_i$，$y$ 后面第 $i$ 个 G 是 $v_i$，那么对于一个子串 $s[l:r]$，$f(t)=\sum|(u_i-l+1)-(r-v_i+1)|$，也就是 $\sum|(u_i+v_i)-(l+r)|$，这是一个关于 $l+r$ 的函数

注意到如果 $l+r$ 每次只改变 $1$，那么这个函数的变化量是非常好算的，可以 $O(1)$ 做，那么我们只需枚举 $x,y$，然后每次将 $l$ 或 $r$ 改变 $1$，遍历所有状态，就可以计算答案了，而这是好做的

由于每个 $l,r$ 只会被一个 $(x,y)$ 对统计到，且 $(x,y)$ 对的个数是 $O(n)$ 的，所以复杂度是 $O(n^2)$

---

18. luoguP9019 - [USACO23JAN] Tractor Paths P [Safe]

题面

有 $n$ 个区间 $[l_i,r_i]$，保证 $l_1<l_2<\cdots<l_n$ 且 $r_1<r_2<\cdots<r_n$，其中有些区间是特殊的

现在以这些区间为点建一张图，相交的区间之间有一条无权无向边

$q$ 次询问，每次给定 $a,b(a<b)$，查询 $a$ 到 $b$ 的最短路，以及有多少特殊区间可能在 $a$ 到 $b$ 的最短路上

$n,q\le2\times10^5$

题解

[Sol]

我们一定是从 $a$ 尽量向右走，那么第一问倍增判断什么时候第一次超过 $b$ 即可

考虑第二问，在 $a$ 到 $b$ 的最短路上的点 $x$，只有可能在第 $\text{dis}(a,x)$ 步出现，也就是只会在一个位置出现，因此我们可以直接统计每个位置有多少种可能

设 $\text{nxt}(a,d)$ 是从 $a$ 开始走 $d$ 步所能到达的最靠右的区间，$\text{prv}(b,d)$ 是 $b$ 开始走 $d$ 步所能到达的最靠左的区间，那么第 $d$ 步的可能数就是 $[\text{prv}(d,\text{dis}(a,b)-d),\text{nxt}(a,d)]$ 内的特殊区间个数，转化成前缀和就可以拆成 $a,b$ 独立的问题，倍增维护即可

复杂度 $O((n+q)\log n)$

---

19. luoguP9020 - [USACO23JAN] Mana Collection [Keter] ✔️

题面

给定一张 $n$ 个点 $m$ 条边的有向图，边形如 $(u_i,v_i,w_i)$，表示从 $u_i$ 走到 $v_i$ 会花费 $w_i$ 单位时间，你可以任意选定起点并开始走路，每个节点 $1$ 单位时间会生产 $k_i$ 的 mana，你到达一个节点时会收割当前节点上的所有 mana（并让这个节点的 mana 归零）

$q$ 次询问，问如果要求你第 $s$ 时刻停止走路，并且你必须处于第 $e$ 个节点，你最多能收集到多少 mana

$1\le n\le18,0\le m\le n(n-1),1\le k_i\le10^8,1\le w_i\le10^9,1\le s\le10^9,1\le q\le2\times10^5$

题解

[Sol]

想不明白了。

倒过来，那么每个节点只跟最后一次经过的时间有关

我们可以计算每倒着走一步浪费的 mana 数量，也就是当前还没有访问过的节点的 $m_i$ 之和

因此我们可以考虑 dp，注意到顺着转移，每次在倒着走到一个点不是很好搞，所以我们倒着转移，在路径前面加一个点，这样还没有访问过的节点就是确定的

令 $f_{S,i}$ 表示我们访问了集合 $S$，且倒着走第一个访问的是 $i$，最少浪费了多少 mana，每次转移枚举在前面加的点 $j$，就有：

$$f_{j,S+\{j\}}\leftarrow f_{i,S}+dis(i,j)\times sumk_S$$

其中 $sumk_S$ 表示 $S$ 内所有节点的 $k$ 之和，设 $ans_{s,e}$ 表示询问 $s$ 和 $e$ 的答案，有转移式：

$$ans_{s,e}\leftarrow sumk_S\times s-f_{S,e}$$

后面这个就是一个一次函数取 max，可以对每个 $e$ 维护直线凸包来解决

现在唯一的问题就是我们并没有保证访问的节点的总时间 $\le s$，但我们观察一下，如果总时间 $>s$，那么最后访问的那个节点相当于在一个负的时间访问了，总贡献为负，我们把它直接删掉一定更优，因此不用保证这件事情

那么总复杂度就是 $O(n^3+2^nn^2+q\log n)$

---

20. luoguP9021 - [USACO23JAN] Subtree Activation P [Safe]

题面

给定一棵 $n$ 个点的树，点有 01 点权，初始都为 0，你每次操作可以翻转一个点的点权，要求你求出满足如下条件的操作序列的最小长度：

按这个操作序列翻转点权，对于任意 $r$，存在某一时刻满足 $r$ 子树内的节点都为 1，且 $r$ 子树外的节点都为 0，并且在所有操作进行完之后，所有节点都为 0

$2\le n\le2\times10^5$

题解

[Sol]

令 $f_u$ 表示满足 $u$ 的子树内所有限制，且需要撤销的最小步数，$g_u$ 表示满足 $u$ 子树内所有限制，且不需要撤销的最小步数

对于 $f$，一种暴力的思路是我们对每个儿子都做完再撤销，然后最后将 $u$ 的子树整个填满再撤销，但是显然可以省东西，我们做的最后一个儿子 $v_1$ 可以不撤销，并且填满 $u$ 的子树之后最后一个撤销的儿子 $v_2$ 也可以多满足一些限制，容易发现这就是 $g$ 的值，枚举 $v_1,v_2$ 后直接转移即可，注意特判一下 $v_1=v_2$ 的情况

$g$ 的情况更简单，我懒得写了。

复杂度 $O(n\log n)$ 或 $O(n)$

---

21. luoguP9130 - [USACO23FEB] Hungry Cow P [Euclid] ⭐

题面

有一个人在炫饭。

对于每个 $i$，第 $i$ 天早上会凭空出现 $a_i$ 碗饭

每天晚上，如果当前还有饭，那么这个人会炫掉一碗饭

初始所有 $a_i$ 都为 $0$，接下来有 $q$ 次修改，给定 $x_i,y_i$，执行 $a_{x_i}\leftarrow y_i$，每次修改后你要输出这个人能炫到饭的天的编号之和，对 $10^9+7$ 取模

$1\le q\le10^5,1\le x_i\le10^{14},0\le y_i\le10^9$

题解

[Sol]

考虑这种往后推的题，一般可以写一个被覆盖的充要条件

我们设 $sum_i$ 表示 $i$ 时刻及之前出现的饭的总数，那么 $i$ 时刻有饭吃的充要条件就是存在一个 $x$ 使得 $sum_i-sum_{x-1}\ge i-x+1$，也就是 $sum_i-i\ge sum_{x-1}-(x-1)$

那么我们反过来，求炫不到饭的编号之和，那么也就是 $sum_i-i$ 的前缀和的下标之和，而这就是线段树维护前缀最小值的经典套路，具体地：

对每个点，我们维护最小值 $mn$，以及 $val$，表示右儿子中值 $<mn_{lc}$ 的前缀最小值下标之和

如果我们能算出这个，我们就能支持查询对于一个线段树上的节点代表的区间，这里面值 $<x$ 的前缀最小值下标之和，我们每次将 $x$ 和 $mn_{lc}$ 子树，不难发现我们只用进一边的子树，这样单次查询复杂度是 $O(\log V)$ 的

考虑怎么维护 $val$ 值，我们直接每次 pushup 时重新求一遍即可，这样总复杂度是 $O(\log^2V)$ 的

区间加是容易接入到这里面的，那么我们就获得了一个 $O(q\log^2V)$ 的做法，但这东西再加上动态开点就太难写了

因此，我们可以将所有修改的时间离散化，那么大小相邻的两个数之间一定是一个公差为 $-1$ 的等差数列，所以我们就只用对 $O(q)$ 个段建线段树，复杂度 $O(q\log^2q)$

---

22. luoguP9131 - [USACO23FEB] Problem Setting P [Euclid]

题面

有 $m$ 个人做 $n$ 道题，现在已知第 $i$ 个人认为第 $j$ 道题 难/简单，求有多少题目序列（也就是你可以选出一些题目并对它们进行重排），使得不存在一个人认为序列中第 $x$ 道题难，且序列中第 $y(y>x)$ 道题简单，对 $10^9+7$ 取模

$1\le n\le10^5,1\le m\le20$

题解

[我的做法]

人数非常少，考虑状压

首先有一个显然的 dp 就是 $f_S\rightarrow f_T(S\subseteq T)$，如果有多道状态相同的题目，我们可以记录次数然后赋一个点权来把它们合并起来

但是这样复杂度太高了，

[acniu 做法]