task | Flamiblog

[TOC]

1. CF1772F2 - Magician and Pigs (Hard Version) [Keter] ⭐

题意

n op, op = {
 1 x, create x HP obj
 2 x, forall obj -x HP
 3, repeat all prev op
}
after all op, print #{HP>0 obj}
n[1,8e5], x[1,1e9]

题解

Sol

对于之前没有 2 操作的 3 操作，容易处理

考虑一次操作相当于创建两个平行世界，第一个平行世界中所有 obj 不变，第二个平行世界中所有 obj 都减去某一个定值 $v_i$，这个定值为之前所有 2 操作加上 3 操作的 buff 之后减去的数

有 $v_i\ge2v_{i-1}$，因此最多有 $O(\log x)$ 次有用的 3 操作，因为如果 $v_i\ge10^9$ 减一次就全寄了

那么我们相当于对于每一个 1 操作产生的 obj，设它之后的 3 操作的 $v$ 为 $v_1,v_2,\cdots,v_k$，我们要从中选出一个可空的子集使得它的和 $<x$

由于 $v_i\ge2v_{i-1}$，所以 $\sum_{jv$ 令 $x\leftarrow x-v$，并将二进制数的这一位设为 1，否则设为 0

不难发现由于有 $\sum_{j<i}v_j<v_i$，$<x$ 的子集个数就是二进制数大小+1（加上空集）

复杂度 $O(n\log x)$

2. CF1771F - Hossam and Range Minimum Query [Keter]

题意

Int a[n]
q Qs: l r, Q min {x|#{x in a[l:r]} odd}
online
n[1,2e5] ai[1,1e9] q[1,2e5]
1.5s,256MB

题解

[我的做法]

我们只要求出来有哪些数出现了奇数次，我们就能求出其中的最小值

如果我们预处理出了每个前缀有哪些数出现了奇数次，那么相当于找到 $[1,l-1]$ 与 $[1,r]$ 第一个不一样的位置

这个可以用 bitset 维护，但直接做空间复杂度是 $O(\frac{n^2}\omega)$ 的，比较大

我们可以只对长度为 $\sqrt n$ 倍数的块维护有哪些数出现了奇数次，每次询问 $O(n\sqrt n)$ 的时间暴力跳，这样空间复杂度 $O(\frac{n\sqrt n}\omega)$，时间复杂度 $O(n\sqrt n+\frac{n^2}\omega)$

需要卡常，询问的时候直接 (bl^br)._Find_first() 会 TLE，必须手写，找到异或值中第一个不同的位置直接跳出

[std 做法]

维护每个前缀有哪些数出现了奇数次，将它们扔到可持久化 trie 里

查询相当于查第 $l-1$ 棵树和第 $r$ 棵树第一个不同的位置

这个可以通过维护子树哈希值来实现，可以线段树上二分

复杂度 $O(n\log a_i)$

3. CF1762F - Good Pairs [Euclid]

题意

Int a[n],k
Q #(l,r)=
{
	exists b = subseq (a[l:r]), a[l],a[r] in b
	forall i, |b[i]-b[i-1]|<=k
}
n[1,5e5] k[0,1e5] ai[1,1e5]
3s,256MB

题解

Sol

观察发现一定子序列要么单调增要么单调降（可以通过调整把拐点干掉），我们不妨只考虑单调增的情况

我们可以从一个 $l$ 开始向右贪心选择，如果 $a_i\in[a_{last},a_{last}+k]$ 那么选择 $a_i$，那么对于每个符合条件的 $(l,r)$，一定存在一种到 $r$ 的方式是在选出的这些数上走，直到某一步直接跳到 $r$

也就是说如果我们设选出的下标为 $id_1,id_2,\cdots,id_x$，存在一个 $id_i$ 使得 $id_i\le r,a_r\in[a_{id_i},a_{id_{i+1}})$

那么我们可以令 $dp_i$ 表示以 $i$ 为 $l$ 的合法数对有多少个，有转移式 $dp_i=dp_{nxt_i}+|\{j\ge i,a_j\in[a_i,a_{nxt_i})\}|$，其中 $nxt_i$ 是下一个在 $[a_i,a_i+k]$ 之间的数

这些都可以用数据结构优化，复杂度 $O(n\log a_i)$

4. CF1739F - Keyboard Design [Safe]

题意

p=perm('a'~'l')
int c[n];str('a'~'l') s[n]
max(\sum_i [\forall j, s[i][j] s[i][j+1] adj in p] c[i]), print p
n[1,1e3],ci[1,1e5],|si|[2,2e3],\sum |si| (,1e3],\forall i,j, si[j]!=si[j+1]
4s,1GB

题解

Sol

一眼题。

每一个字符串必须是一条链，那么问题转化为给定若干 $c_i,s_i$，求一个排列 $p$ 使得 $s_i$ 或 $r(s_i)$ 是 $p$ 的子串的所有 $c_i$ 的和最大

由于 $p$ 是排列，出现 $s$ 一定不出现 $r(s)$，所以可以直接将其拆成两个来看

那我们将对所有建 AC 自动机，然后 $dp_{S,u}$ 表示已经用过的字符集合 $S$，AC 自动机上在节点 $u$ 的最大 $c_i$ 和即可

复杂度 $O(2^{12}\times\sum|s_i|\times12)$

5. CF1749F - Distance to Path [Safe]

题意

tree(n), V weight, init 0
m op:
1. v, Q weight(v)
2. u v k d, \forall dis(x,u->v)<=d, w[x]+=k
n[2,2e5],m[1,2e5],k[1,2000],d[0,20]

题解

Sol

考虑 $d$ 很小，我们可以考虑每次询问的时候暴力找这个点的 $d$ 个祖先，并且根据上面的一些 tag 来算出当前点的点权

那么我们打 $(u,d,k)$ 的 tag 表示对 $u$ 子树内 $dis(u,v)\le d$ 的所有 $v$ 的点权 $+k$

那我们进行一些手玩，发现一次修改相当于：

给 $u\rightarrow v$ 上的每一个不是 lca 的点打上 $(d,k)$ 与 $(d-1,-k)$ 的 tag
给 lca 的 $x(0\le x\le d)$ 级祖先打上 $(d-x,k)$ 的 tag，并且如果其父亲存在且 $d-x-2\ge0$，再打上 $(d-x-2,k)$ 的 tag

第一个操作可以通过数据结构做到 $O(nd^2\log n)$，优化一下就是 $O(nd\log n)$

第二个操作可以在数组上暴力修改，查询是 $O(nd^2)$，应该可以做到 $O(nd)$

总复杂度 $O(nd\log n)$

6. CF1779G - The Game of the Century [Euclid]

题意

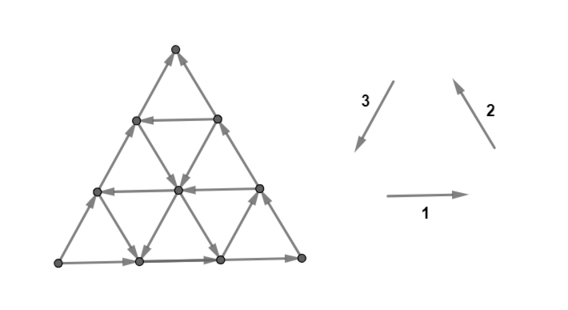
如图。

一个等边三角形，取每边的 $n$ 等分点，用 $3n-3$ 条直线将其分为 $n^2$ 个小等边三角形，算上三角形三条边一共 $3n$ 条

分割的 $3n$ 条直线，每条直线都有一个方向，将每个交点看成点，每个小线段看成有向边，方向是所在直线的方向

问最少翻转多少条边（注意不是直线）的方向使得这张图强联通

$1\le n\le10^5$

题解

Sol

结论：如果我们有一个环，那么环上及环围起来的所有点都强联通

证明：显然，考虑每条直线的两种方向。

所以如果最外面三条边形成一个环，那么答案为 0，判掉

否则，我们取对于顺时针、逆时针，三个方向上最靠外的直线，一共六（ $2\times3$ ）条，经过大量手模，我们发现它们一定会形成长成如下的样子（或类似，但其实本质都相同）的强联通分量：

答案就是 min(n,min(橙+绿,紫+粉))，别问我为什么，多手模几次。

复杂度 $O(n)$

7. CF1770F - Koxia and Sequence [Keter] ✨

题意

set(Int a[n]) S:{a|\forall{i}ai>=0, \sum a=x, \or a=y}
def f(a)=\xor a
print \xor_{a\in S}f(a)
n[1,2^40),x[0,2^60),y[0,2^20)

题解

Sol

what magic is this.

对于每一个 $i$，$a_i=t$ 的方案数一定都相等，因此如果 $n$ 是偶数答案为 0

否则我们需要求出满足 $a_1=t$ 的序列个数，如果是奇数那么就给答案异或上 $t$

按位拆开，变成求满足 $a_1$ 的第 $i$ 位为 $1$ 的序列个数

那么我们容斥一下，把 $\bigvee a_i=y$ 改为 $\bigvee a_i\subseteq y$，定义这样的答案为 $f(y)$，通过一些容斥，我们可以得到答案就等于 $\bigoplus_{y^\prime\subseteq y}f(y^\prime)$

因此，我们想对每一对 $(i,y^\prime)$ 分别计算答案，也就是 $\sum_{t_1+t_2+\cdots+t_n=x}[\forall t_i\subseteq y^\prime][\{i\}\in t_1]$

我们将 $t_1$ 减去 $2^i$，就可以得到 $\sum_{t_1+t_2+\cdots+t_n=x-2^i}[\forall_{2\le i\le n}t_i\subseteq y^\prime][t_1\subseteq y^\prime-2^i]$

而 $[a\subseteq b]=\binom ba\bmod2$，所以我们可以直接把答案写成 $\sum_{t_1+t_2+\cdots+t_n=x-2^i}\binom{y-2^i}{t_1}\prod_{2\le i\le n}\binom{y^\prime}{t_i}$

根据某个结论（范德蒙德卷积）：$\sum_{t_1+t_2+\cdots+t_n=m}\prod\binom{a_i}{t_i}=\binom{\sum a_i}{m}$

因此答案就是 $\binom{ny^\prime-2^i}{x-2^i}\bmod2$

所以我们可以 $O(1)$ 计算每对 $(i,y^\prime)$，复杂度 $O(y\log y)$

不知道怎么想到的，非得要总结的话大概是 $\binom nm$ 和 $[n\subseteq m]$ 可以互相转化？但是平时谁没事想着转化这个啊。

8. CF1731F - Function Sum [Safe]

题意

f(Int a[n],i)=|{j|j<i,aj<ai}|
g(Int a[n],i)=|{j|j>i,aj>ai}|
set(Int a[n]) S={a|\forall 1<=ai<=k}
print \sum{a\in S,f(a,i)<g(a,i)} ai, mod 998244353
n[1,50],k[2,998244353)

题解

Sol

垃圾题。

$ans=\sum_{i=1}^n\sum_{y=0}^{i-1}\sum_{z=y+1}^{n-i}\binom{i-1}y\binom{n-i}z\sum_{x=1}^k(x-1)^y(k-x+1)^{i-1-y}(k-x)^zx^{n-i-z+1}\\$

直接对 $x$ 插值，复杂度 $O(n^4)$

9. CF1783E - Game of the Year [Euclid]

题意

$n$ 个人，A 和 B 会打这些人。

对每个人的打都是一个独立的过程，这个过程是这样的：A 先打 $k$ 下，B 再打 $k$ 下，这样轮流

第 $i$ 个人死当且仅当被 A 累计打了 $a_i$ 下或被 B 累计打了 $b_i$ 下

问有多少 $k$ 使得每个人都是 A 打死的

$1\le n\le2\times10^5,1\le a_i,b_i\le n$

题解

[赛时做法]

$k$ 满足条件当且仅当 $\forall\lfloor\frac{a_i-1}k\rfloor\le\lfloor\frac{b_i-1}k\rfloor$

直接暴力整除分块，复杂度 $O(n\sqrt a_i)$，过不去。

[std]

我们首先把 $a_i\le b_i$ 的全都筛掉，这些一定满足条件

然后对于一个 $k$，如果 $(a,b)$ 要满足条件，一定存在一个 $i$ 使得 $a_j\le(i+1)k$，$b_j>ik$，也就是任何 $[b_i,a_i]$ 的区间不跨过 $ik$ 与 $ik+1$ 的分割

那么差分一下然后每次 $O(\frac nk)$ 判一下就行了

复杂度 $O(n\ln n)$

10. CF1783F - Double Sort II [Euclid]

题意

两个排列 $a,b$，一次操作你可以选定一个 $i$，找到满足 $a_x=i$ 和 $b_y=i$ 的 $x,y$，然后执行 swap(a[x],a[i]),swap(b[y],b[i])

求将 $a,b$ 升序排序的最小步数，并构造方案

$2\le n\le3000$

题解

Sol

考虑一次操作就相当于把 $x$ 在环上的前驱连向 $x$ 在环上的后继，$x$ 独立出来成自环，最后的目标是让所有数都成自环

我们把每个长度大于 $1$ 的环都看成一个集合，一次操作相当于在 $a$ 中和 $b$ 中分别将这个数删掉，如果删掉这个数之后出现大小等于 $1$ 的集合那么将这个集合也删掉

所以一次操作可能删一个数，也可能删两个数，而我们删的数都是固定的，所以要尽可能删两个数的更多

而我们的限制只有在同一个环内的数不能全是删两个的（因为最后一定长为 $1$ 的那个一定被连带删掉了），这个可以用网络流解决

复杂度 $O(挺快)$，大概是 $O(n\sqrt n)$

11. CF1783G - Weighted Tree Radius [Euclid]

题意

$n$ 个点的树，点有点权 $a_i$，定义 $dis(u\rightarrow v)$ 为 $u$ 到 $v$ 路径上的边数 $+a_v$

定义树的半径为 $\min_u\max_vdis(u\rightarrow v)$

$m$ 次修改，每次 $a_{v_i}\leftarrow x_i$，

$2\le n\le2\times10^5,1\le m\le10^5$

题解

Sol

无聊。

相当于每个节点上挂了一个边权为 $a_i$ 的叶子，由于一条路径只有两端的边是非 1 权值，所以知道直径之后半径就很好算

直径直接放线段树上维护就行了，用两个点集合并直径的经典结论（$C_4^2$ 种直径端点选法）

复杂度 $O(m\log^2n)$

12. CF1768F - Wonderful Jump [Keter] ✔️

题意

$n$ 个点，有一个数列 $a_1,a_2,\cdots,a_n$

建图，对每个 $i<j$，$i$ 向 $j$ 连一条长为 $\min(a_i,a_{i+1},\cdots,a_j)\times(j-i)^2$ 的有向边

求以 $1$ 为源的单源最短路

$1\le n\le4\times10^5,1\le a_i\le n$

题解

Sol

下次多想一会再看题解。

不过我好像还读错题了阿！

感觉还有点意思。

转移边一共有 $O(n^2)$ 条，太多了，我们考虑缩减一下

如果 $[i,j]$ 中的某个最小值为 $a_k$ 且 $i\neq k,j\neq k$，那么 $i\rightarrow j$ 不如 $i\rightarrow k\rightarrow j$，因此每条边的权值可以改为 $a_i(j-i)^2$ 或 $a_j(j-i)^2$，且 $(i,j)$ 内不能包含 $\le\min(a_i,a_j)$ 的边

考虑如果一条边的权值 $\ge n(j-i)$，那一定不如一步一步走过去（每次走 $j-i=1$ 的边），因此任意一条有用的边一定满足 $a_i(j-i)\le n$

那么我们分析一下此时有用的边数：

对于 $a_i\le\sqrt n$ 的点，它有用的边一定不经过上一个 $a_j=a_i$ 以及下一个 $a_j=a_i$ 的 $j$，因此以 $a_i$ 为权值的有用的边总数不超过 $O(n)$，那么这部分总共的边数就是 $O(n\sqrt n)$
对于 $a_i>\sqrt n$ 的点，它有用的边一定在 $[i-\sqrt n,i+\sqrt n]$ 的范围内，否则 $a_i(j-i)>n$，因此每个位置最多有 $O(\sqrt n)$ 条有用的边，这部分总共的边数就是 $O(n\sqrt n)$

转移边数 $O(n\sqrt n)$，比较好实现，总复杂度 $O(n\sqrt n)$

13. CF1198F - GCD Groups 2 [Keter] ✔️

题面

长为 $n$ 的数列 $a_1,a_2,\cdots,a_n$，将其分为两个非空集合，使得每个集合的 $\gcd=1$，给出构造或判断无解

$1\le n\le10^5,1\le a_i\le10^9$

题解

Sol

以下令 $k=\omega(a)$

如果有一组解，那么我们分别从两组中任取一个元素 $x,y$，对于两个集合，一定都可以找出一个大小不超过 $k$ 的子集，使得这个子集的 $\gcd=1$

那么剩下的元素都可以随便选，做一个很松的估计，两个数不能在不同的集合的概率至多有 $\frac{k^2}{n^2}$

对于 $\frac kn>\frac12$，也就是 $n\le2k$，可以直接暴力

否则，我们随机取 $q$ 次 $x,y$，每次判断这两个数是否可能在不同的集合，这个可以用 $dp$ 来判断，令 $dp_{i,S,T}$ 表示考虑前 $i$ 个数，第一个集合中 $S$ 中的质因子还活着，第二个集合中 $T$ 的质因子还活着，容易发现复杂度是 $O(qn2^{2k})$ 的，复杂度有点高

考虑对于每个质因子，最多只用考虑 $2k$ 个不整除它的数，因此我们可以把数的个数缩减到 $O(k^2)$，复杂度就是 $O(q(2^{2k}k^2+nk))$，可以接受

错误率是 $O(\frac1{4^q})$

14. CF1617E - Christmas Chocolates [Euclid] ⭐

题面

数列 $a_1,a_2,\cdots,a_n$，定义 $f(x,y)$ 为：

你可以进行操作，一次操作可以选择一个 $k$ 使 $2^k\ge a_x$，并将 $a_x$ 变成 $2^k-a_x$

使 $a_x=a_y$ 的最小操作次数为 $f(x,y)$

对于所有 $i,j$，求 $f(a_i,a_j)$ 的最大值，输出最大值与此时的 $i,j$

$2\le n\le2\times10^5$

题解

[我的做法]

就硬手模。

考虑操作可逆。

我们可以发现，除非将一个数减成 0，否则这个数的 lowbit 一直不会变，我们将这些位删掉不考虑

进行两次操作相当于在这个数的最高位 1 前面任意添加一段 1，或者把最高的 1 段删掉一个前缀

转换到差分数组上相当于将第 $1$ 位反转以及第 $k$ 位翻转

那么如果 $\text{lowbit}(x)\neq\text{lowbit}(y)$，一定是将两个数都变成 0

否则，答案就是差分数组删掉 lcp 后 1 的个数之和

（是的，很抽象）

那么对于第一种情况，我们可以按 lowbit 分类，然后容易统计

对于第二种情况，我们可以对每种 lowbit 开一棵 trie，然后在树上统计

复杂度 $O(n\log a_i)$，空间复杂度 $O(n\log a_i)$

[题解做法]

如果 $x+y=2^k$ 那么就在 $(x,y)$ 之间连边，建出无向图

考虑对于任意 $x$，只有一个 $y$ 满足 $y<x,x+y=2^k$，所以这个图是一棵树

那么我们相当于要求这棵树上 $n$ 个点之间的最大距离，也就类似于树的直径

不难发现，这个树的深度只有 $\log a_i$

一种方法是只建 $n$ 个点到根（0）路径上的点，这样只有 $O(n\log a_i)$ 个点，可以接受

或者用求最远点的方法求直径，算距离的时候暴力跳父亲，复杂度也是 $O(n\log a_i)$

15. CF1672H - Zigu Zagu [Euclid]

题面

对于一个 01 串 $s$，定义 $f(s)$ 为：

一次操作可以删掉一个 01 交替的子串，剩下两部分拼起来，$f(s)$ 为将其删空的最少操作次数

给定一个长为 $n$ 的 01 串 $a$，$q$ 次询问，每次给定 $l,r$，询问 $f(a[l:r])$

$1\le n,q\le2\times10^5$

题解

Sol

一次操作我们一定是删除一段极长的交替段，那么这个交替段两端一定满足 $a_{l-1}=a_l,a_r=a_{r+1}$，接着 $a_{l-1}$ 和 $a_{r+1}$ 会合到一起

那么我们考虑满足 $a_i=a_{i+1}$ 的数量 $x$，如果 $a_{l-1}=a_{r+1}$，进行 $[l,r]$ 操作会让 $x$ 减 $1$，否则会让 $x$ 减 $2$

也就是说，我们把所有满足 $a_i=a_{i+1}$ 的都提出来，如果有 $=0$ 和 $=1$ 的相邻，那我们可以把这两个同时消掉，否则我们只能对每个单独消

我们发现，如果同时存在 $=0$ 的 $=1$ 的，那么必定存在一个位置 $=0$ 的和 $=1$ 的相邻，因此答案是 $[l,r]$ 内相邻的 0 和相邻的 1 的个数的最大值

复杂度 $O(n+q)$

16. ARC153D - Sum of Sum of Digits [Safe]

题意

给定 $a_1,a_2,\cdots,a_n$，求 $\min\sum f(a_i+x)$，其中 $f(x)$ 表示 $x$ 的各位数字之和

$1\le n\le2\times10^5,1\le a_i<10^9$

题解

Sol

trick 题。

我们按后 $x$ 位从大到小排序，进位的一定是一个前缀，这样就可以放到状态里了

令 $dp_{i,j}$ 表示后 $i$ 位，按后 $i$ 位排序后长为 $j$ 的前缀都进位了的最小数字和

转移的时候直接枚举这一位选的是什么就可以了

复杂度 $O(10n\log a_i\log n)$，有很多显然的优化空间，应该可以至少把 $\log n$ 优化掉

17. CF1782F - Bracket Insertion [Keter] ✔️

题意

你有一个括号串 $s$，初始为空，进行一次操作会从 $|s|+1$ 个位置中随机选择一个，以 $p$ 的概率插入 ()，以 $1-p$ 的概率插入 )(

求做 $n$ 次操作后形成的串为合法括号串的概率

$1\le n\le500,0\le q\le10^4$

题解

Sol

完全不懂。

感觉这题主要在于怎么划分成独立的问题。

[xcyle 做法]

对于一个括号串，我们枚举它第一个字符是和哪个字符一起被加入的，设其为 $k$，那么剩下的操作要么完全在 $[1,k]$ 内部或完全在 $[1,k]$ 外部，因此可以将其划为两个看起来有点独立的问题

此时 $[1,k]$ 内部的操作需要保证最小前缀和 $\ge-1$，$[1,k]$ 外部的操作需要保证最小前缀和 $\ge0$，因此我们还需要记录需要保证最小前缀和的限制

令 $dp_{i,j}$ 表示操作 $i$ 次，最小前缀和 $\ge-j$ 的概率，那么我们有 $dp_{i,j}\leftarrow p\times dp_{k-1,j+1}\times dp_{i-k,j}\times\binom ik$ 与 $dp_{i,j}\leftarrow (1-p)\times dp_{k-1,j-1}\times dp_{i-k,j}\times\binom ik$

直接转移即可，复杂度 $O(n^3)$

[tyq 做法]

现将答案乘上 $\prod(2i-1)$

我们只关心前缀和的集合，设其为 $S$，那么我们对于 $S$ 中的每一个元素 $x$，会有 $p$ 的概率向 $S$ 中加入 $x$ 和 $x+1$，会有 $q$ 的概率向 $S$ 中加入 $x$ 和 $x-1$，且我们不能向 $S$ 中加入负数

我们发现，每个数生出来的数都是相对独立的，我们可以将它们的操作用组合数合起来

那么我们设计状态：$f_{i,j}$ 表示一开始 $S=\{j\}$，做 $i$ 次操作后 $S$ 中没有负数的概率，$g_{i,j}$ 表示一开始 $S=\{j,j\}$，做 $i$ 次操作后 $S$ 中没有负数的概率

我们有：$f_{i,j}=\sum_{0\le k0]qg_{k,j}f_{i-1-k,j-1}\binom{i-1}k$，$g_{i,j}=\sum_{0\le k\le i}f_{k,j}f_{i-k,j}\binom ik$

复杂度 $O(n^3)$

18. CF1720E - Misha and Paintings [Keter]

题面

一个 $n\times n$ 的矩阵 $a$，矩阵里有数 $a_{i,j}$，每次你可以选择一个连续的正方形子矩形，将其中的数全覆盖成某个值（每次操作都可以重新选）

问使得矩形中恰好有 $k$ 种不同的数的最小操作次数

$1\le n\le500,1\le k\le n^2$

题解

Sol

不是，这种题是怎么猜到结论的。

设一开始有 $d$ 种不同的数，若 $d\le k$，那么答案显然是 $k-d$

否则，我们可以证明答案不超过 2：

$\begin{bmatrix}1&3&6&10&15&\cdots\\3&2&5&9&14&\cdots\\6&5&4&8&13&\cdots\\10&9&8&7&12&\cdots\\15&14&13&12&11&\cdots\\\vdots&\vdots&\vdots&\vdots&\vdots&\ddots\end{bmatrix}$

按这样给矩形的每个格子标号。

首先，如果我们覆盖的两个子矩形已经确定了，我们设它们组成的图形是 $S$，设删掉 $S$ 之后剩下的数一共有 $f(S)$ 种，那么最后的不同数种数是 $f(S)+[0,2]$，其中 $[0,2]$ 是由这两个子矩形覆盖成的数提供的，可以任意选择

而我们发现，这样将矩形标号之后，对于任意 $x$，$\le x$ 的格子形成的图形 $S_x$ 都一定能用两个正方形覆盖出来，而标 $x$ 的格子最多只有两个，因此 $f(S_x)\le f(S_{x-1})+2$，因此中间的差可以用 $+[0,2]$ 覆盖

（注意上面的证明是对 $x\neq\frac12p(p+1)$ 的，对于 $x=\frac12p(p+1)$ 的情况把 $2$ 改成 $1$ 后同理）

因此我们证明了答案 $\le 2$

判一下答案是不是 $0/1$ ，$1$ 的情况枚举正方形边长再差分统计每个正方形能干掉多少种数即可

复杂度 $O(n^3)$

19. CF1615F - LEGOndary Grandmaster [Keter]

题面

$s,t$ 是长度相同的 01 串，定义 $f(s,t)$：

一次操作可以将 $s$ 中某一组相邻的 00 或 11 取反，将 $s$ 变为 $t$ 的最少操作次数为 $f(s,t)$，如果无法变为 $t$ 则 $f(s,t)=0$

给定两个由 0，1，? 组成的字符串 $a,b$，对于所有将 ? 填成 01 的方式，求 $\sum f(a,b)$

对 $10^9+7$ 取模

$2\le n\le2000$

题解

Sol

观察发现（是的我也不知道是怎么观察出来的）：将偶数位取反后操作就相当于交换相邻两个数

那么答案就是对应排名的 1 的位置之间的距离

然后可以分为两派做法：

dp 做法，看了一些人的提交，貌似两两不同，说说我的。想象有两个哨兵 $X,Y$ 分别在 $a$ 和 $b$ 上走路，每次 $X$ 先向右走，找到第一个 1，然后 $Y$ 向右走，找到第一个 1，给答案加上 $X,Y$ 的位置差，用 dp 模拟这个过程，令 $f_{i,j,X/Y}$ 表示当前 $X$ 在 $i$，$Y$ 在 $j$，正在移动的是 $X$ / $Y$ 的方案数，$g_{i,j,X/Y}$ 表示 $\cdots$ 的 $f(a,b)$ 之和
组合数做法，统计每一个 $(a_i,b_j)$ 是排名相同的 1 的方案数，那么就需要算一个形如 $\sum\limits_{i=0}^\infty\binom ni\binom m{i+c}$ 的东西，这个等于 $\sum\limits_{i=0}^\infty\binom n{n-i}\binom m{i+c}$，根据范德蒙德卷积也就是 $\binom{n+m}{n+c}$

两种方法复杂度都是 $O(n^2)$

20. SDOI2013 D?T? - 森林 [Keter]

题面

forest(n,m), node weight ai
q op:
1. Q x y k, print(kth(x->y))
2. L x y, addedge (x,y)
online
n,m,q[1,8e4], ai[1,1e9]

题解

Sol

如果没有加边，那么可以用主席树解决这个问题，具体地每个点基于父亲的版本建一棵权值线段树，维护这个点到根的桶，然后查询的时候分四个节点在上面二分即可

考虑加边不是很好维护，而挂一个叶子比较好维护，所以我们可以启发式合并维护加边操作

复杂度 $O(n\log^2 n)$

21. CF911G - Mass Change Queries [Euclid] [Keter] ⭐

题面

Int a[n]
q op:
l r x y, \forall ai=x, i in [l,r], ai:=y
print a after all op
n,q[1,2e5], ai,x,y[1,100]
bonus: ai,x,y[1,n]

题解

[弱智做法]

这个操作看起来不是很可以打 tag 的样子，于是我们扫描线，改成每次加入一个操作或删除一个操作

我们发现这样还不是很好做，所以我们直接对时间轴建线段树，每个节点维护一个 $O(\max a_i)$ 的数组，表示每种数走完 $[l,r]$ 中的操作后会变成什么

复杂度 $O(n\max a_i\log n)$

[高明做法（来自 CF editorial 的某个 comment）]

对每种数建一个数据结构，维护这种数的所有出现位置，那么我们需要这个数据结构支持：取出 $[l,r]$ 内的所有数以及合并操作

我们发现使用动态开点线段树可以完成这件事情，合并的时候按正常线段树合并（$O(交集)$）就是对的，复杂度分析和正常线段树合并一样，一个节点只在它被合并到其他节点上的时候贡献复杂度，每个点的贡献都是 $O(1)$，而最多有 $O((n+q)\log n)$ 个节点，所以复杂度 $O((n+q)\log n)$

22. luoguP7844 -「dWoi R2」FFT / 狒狒贴 [Euclid]

题意

给定长为 $2^n$ 的序列 $a_0,a_1,\cdots,a_{2^n-1}$，求对 $a$ 做 $k$ 次 DFT 的结果

$\text{DFT}(b)_i=\sum\limits_{j=0}^{2^n-1}b_j\omega^{ij}\bmod998244353$

其中 $\omega\equiv3^\frac998244352{2^n}\pmod{998244353}$

$1\le n\le17,1\le k\le10^{18},0\le a_i<998244353$

题解

Sol

诈骗。

考虑 DFT 两次和 DFT 再 IDFT 很像，所以我们尝试推一下

设 $\text{DFT}(a)=b,\text{DFT}(b)=c,N=2^n$

$\begin{aligned}c_i&=\sum_{j=0}^{N-1}b_j\omega^{ij}\\&=\sum_{j=0}^{N-1}\sum_{k=0}^{N-1}a_k\omega^{jk}\omega^{ij}\\&=\sum_{k=0}^{N-1}a_k\sum_{j=0}^{N-1}\omega^{j(i+k)}\\&=\sum_{k=0}^{N-1}a_k\sum_{j=0}^{N-1}(\omega^{i+k})^j\\&=Na_{N-i}+\sum_{k\neq N-i}\frac{(\omega^{i+k})^N-1}{\omega^{i+k}-1}\\&=Na_{N-i}\end{aligned}$

所以做两次 DFT 相当于将 $a[1:N-1]$ reverse 并给所有数 $\times N$

然后就随便做了。

复杂度 $O(n2^n)$

[附件]

IDFT 的推导过程 $\begin{aligned}c_i&=\sum_{j=0}^{N-1}b_j\omega^{-ij}\\&=\sum_{j=0}^{N-1}\sum_{k=0}^{N-1}a_k\omega^{jk}\omega^{-ij}\\&=\sum_{k=0}^{N-1}a_k\sum_{j=0}^{N-1}\omega^{j(k-i)}\\&=\sum_{k=0}^{N-1}a_k\sum_{j=0}^{N-1}(\omega^{k-i})^j\\&=Na_i+\sum_{k\neq i}\frac{(\omega^{k-i})^N-1}{\omega^{k-i}-1}\\&=Na_i\end{aligned}$

单位根反演

$[n|a]=\frac 1n\sum_{k=0}^{n-1}\omega^{ak}_n\\$

原理：

$\frac 1n\sum_{i=0}^{n-1}(\omega^a_n)^k$，当 $n|a$ 时 $\omega^a_n=1$，特判

LOJ6485 - LJJ 学二项式定理

$\begin{aligned}&\sum_{i=0}^n\binom nis^ia_{i\bmod4}\bmod998244353\\\equiv&\sum_{x=0}^3a_x\sum_{i=0}^n[i\bmod4=x]\binom nis^i\\\equiv&\sum_{x=0}^3a_x\sum_{i=0}^n[4|i-x]\binom nis^i\\\equiv&\sum_{x=0}^3a_x\sum_{i=0}^n\binom nis^i\frac14\sum_{y=0}^3\omega^{(i-x)y}_4\\\equiv&\frac14\sum_{x=0}^3\sum_{y=0}^3a_x\omega_4^{-xy}\sum_{i=0}^n\binom nis^i(\omega_4^y)^i\\\equiv&\frac14\sum_{x=0}^3\sum_{y=0}^3a_x\omega_4^{-xy}(1+s\omega_4^y)^n\\\end{aligned}$

然后就可以 $O(16\log n)$ 计算了

23. luoguP5312 - [Ynoi2011] 竞赛实验班 [Euclid]

题面

Int a[n]
q op:
1. x, a.push_back(x)
2. l r, print sum a[l:r]
3. x, foreach ai := ai xor x
4. sort a
n,m[1,1e5], x,ai[0,1e9]

题解

Sol

没有 4 操作的情况可以拆位来做，非常简单。

没有 3 操作的情况，那么序列一定是一个前缀是有序的，剩下的是无序的，可以拆成这两部分分别用数据结构维护，遇到一次 4 操作就将无序的部分合并进有序的部分

那如果有 3 操作，序列一定是一个前缀是有序的数列异或上某个东西，剩下的是无序的，我们想拆成两部分分别用数据结构维护

无序的部分相当于没有 4 操作的情况，好做。

有序的部分，考虑一位被异或之后再排序，相当于这一位是 1 的排在这一位是 0 的后面，可以尝试用 01-trie 来维护

由于异或是对每一位分别来的，所以我们 trie 上的节点需要对每一位维护子树内这一位为 1 的数有多少个

这里有两种维护方式，本质差不多

[丑陋方式（我的方式）]

我们比较懒，把异或和排序都打成一种 lazytag 的东西，维护 sorttime 和 time 两个标记，分别表示上一个处理了的排序操作的时间戳和上一个处理了的异或操作的时间戳。为了能做，我们需要保证 time 必须大于 sorttime

我们再对每个节点维护四个指针（实际上只有两个儿子，每个儿子有两个指针指向它） lc,rc,0c,1c，分别表示当前节点的左儿子（序列中排在左边的），右儿子（同理），0 儿子（就是 trie 上走标着 0 的边到的儿子），1 儿子（同理），这样我们就可以打 sorttime 标记了

剩下的操作就比较容易了

[优美方式（题解方式）]

维护两个全局标记 tag1 和 tag2，分别表示从开始到上一次排序的时候全局总共异或的数，以及从开始到现在全局总共异或的数

有了这些，到一个节点的时候就可以判断哪个儿子在序列左边了，就不用那些乱七八糟的标记下传了

上述两种维护方式空间复杂度都是 $O(n\log^2 a_i)$ 的，看起来不是很稳，但能过

我们当然是有优化方式的（我没写）：

对 trie 压位，把只有一个儿子的节点压起来，这样每次插入一个数只会产生 $O(1)$ 个新节点，空间复杂度去掉一个 $\log$
我们发现另一只 $\log$ 在于对每一位维护子树中出现次数，而每一位是独立的，因此我们可以只维护一位的值，做 $\log$ 次（对每一位分别做一次），这样就又去掉一个 $\log$，时间复杂度也不会变

最后时间复杂度 $O(n\log^2a_i)$，空间复杂度 $O(n)$

24. CF1787E - The Harmonization of XOR [Safe] ⭐

题面

将 $[1,n]$ 内的数分为 $k$ 个子集，要求每个子集异或和为 $x$，给出构造或判断无解

$1\le k\le n\le2\times10^5,1\le x\le10^9$

题解

Sol

直觉告诉我们这种题一般不需要考虑太奇怪的异或方式，于是我们先将两个数异或 $=x$ 的配对起来，然后你惊奇的发现，剩下的都配不出来了！

首先先算一下 $1\oplus2\oplus\cdots\oplus n$，如果这个东西和 $k$ 个 $x$ 异或起来不相等的话直接无解

我们已经保证了异或和正确，也就是你可以随便选异或为 $x$ 的集合，直到选不出来为止，剩下的数异或和一定是 $0$，也就是说我们只用考虑选异或和为 $x$ 的集合即可，不必考虑剩下的数怎么选

我们可以证明：每次只选大小 $\le2$ 的集合一定是最优的

分两种情况讨论：

$x<\text{highbit}(n)$，那么 $<\text{highbit}(n)$ 的一定都能配对上，对于 $\ge\text{highbit}(n)$ 一定要在内部选，因此我们可以直接将这些数都减掉 $\text{highbit}(n)$，转化为规模更小的问题，归纳证明，不难发现，这样减一定可以减到 $x\ge\text{highbit}(n)$ 的情况
$x\ge\text{highbit}(n)$，那么 $\ge\text{highbit}(n)$ 的数一定要和 $<\text{highbit}(n)$ 的数配对，所以答案上界是 $\ge\text{highbit}(x)$ 的数的个数，而对于任意 $y\ge\text{highbit}(n)$，$y\oplus x$ 一定 $<\text{highbit}(n)$ 并且互不相同，因此这个上界可以通过只选大小 $\le2$ 的集合取满

复杂度 $O(n)$

25. CF1787F - Inverse Transformation [Safe]

题面

对于一个排列 $a$，定义一个排列 $f_1(a)$ 满足 $f_1(a)_x=a_{a_x}$，定义 $f_i(a)=f_{i-1}(f_{i-1}(a))$

对于一个排列 $a$，定义 $\sigma(x)=a_x$，$g(x)$ 是最小的满足 $\underbrace{\sigma(\sigma(\ldots \sigma}_{m \text{个}}(x) \ldots))=x$ 的 $m$

现在给你一个长为 $n$ 的排列，表示 $f_k(a)$，你需要还原一个 $a$ 使得 $\sum\limits_{i=1}^n\dfrac1{g(i)}$ 最小，或者输出无解

$1\le n\le2\times10^5,1\le k\le10^9$

题解

Sol

给你的排列就是每个数原来的排列上走 $2^k$ 步后到达的节点

对于给你的排列上的每一个环，若其大小为 $cyc$，那么我们可以得到原来的环长 $cyca$ 满足 $\{0,2^k,2\cdot2^k,\cdots,(cyc-1)2^k\}$ 在模 $cyca$ 意义下互不相同，且 $cyc\cdot2^k\equiv0\pmod{cyca}$

推一推画一画就可以发现当 $cyc$ 是偶数时，$cyca$ 只能是 $cyc\cdot 2^k$，否则 $cyca$ 可以是 $cyc\cdot 2^x$，其中 $0\le x\le k$

由于要求我们构造的排列环数尽量小，所以我们要尽可能把环套起来，环长偶数的只有一种选择，对于环环长是奇数的，我们直接按个数的二进制套就是最小的，证明显然

复杂度 $O(n)$

26. CF1787G - Colorful Tree Again [Euclid]

题面

给定一棵 $n$ 个点的树，边有边权和颜色

定义一条路径是合法的当且仅当它只包含一种颜色的边，并且包含这种颜色的所有边，并且路径上的点都没有被标记

$q$ 次询问，每次给一个点打上标记/去除标记，操作后你需要输出边权和最大的合法路径

$1\le n,q\le2\cdot10^5$

题解

Sol

显然可以预处理出来有哪些颜色可以组成合法路径

考虑修改一个点会影响到哪些颜色，显然是所有它的邻边的颜色，而这其中只有连向父亲的那一条的 lca 不是当前点，因此我们如果将 lca 相同的点都标号到一起，就可以直接用线段树维护答案了

复杂度 $O(n\log n)$

27. luoguP5101 - [JOI2017 Final] 绳 [Euclid] ✔️

题面

你有一个 $n$ 段的绳子 $a_1,a_2,\cdots,a_n$，每段绳子都有厚度和颜色，初始每段绳子厚度都为 $1$，颜色最多 $m$ 种，且保证每种颜色都出现

你可以进行若干次如下操作：

选择一个 $j$，将 $[a_j,a_{j-1},\cdots,a_1]$ 和 $[a_{j+1},a_{j+2},\cdots,a_n]$ 左对齐合并

当合并两段绳子 $x$ 和 $y$ 时，对于 $x$ 和 $y$ 中的任意一段绳子，你可以花费这段绳子的厚度的代价来将这段绳子染成任意一种颜色，当你染完色后，你需要保证 $x$ 和 $y$ 的颜色相同（设其为 $c$），合并完之后会生成一段颜色为 $c$，厚度为 $x$ 和 $y$ 厚度相加的一段绳子

你希望当绳子只有两段时你希望其中至少一段颜色为 $k$，求最小代价

对 $k=1,2,\cdots,m$ 求答案

$2\le n,m\le10^6$

题解

Sol

被诡异的操作吓到了，但其实拆开来看就清新很多。

首先，我们可以直接把所有染色操作拿到开头来做，不难发现这样不影响答案。

那么我们要将绳子染色，染完色后至多包含两种颜色并且可以通过进行操作来将其缩为两段

一个绳子满足这样的条件当且仅当它的颜色除了第一个连续段和最后一个连续段，剩下的连续段长度都为偶数

证明可以手模一下：

由于我们要无伤，所以每次操作合并的一定都是相同的颜色

对于满足这种条件的情况，我们可以首先通过每次将 $a_1$ 折到 $a_2$ 里来将第一个连续段长度变为 $1$，然后从第二个连续段中点处折，这样显然是可行的

如果内部的连续段有长度为奇数的，一定没办法把这段折起来（怎么折都还会剩一个内部的长为奇数的连续段）

那么我们获得了合法绳子的条件，接下来考虑求答案

假设已经确定了最后的两个颜色 $x$ 和 $y$，那么颜色 $\notin\{x,y\}$ 一定会被染色，答案至少为 $n-cnt_x-cnt_y$

如果我们确定了第一段长度的奇偶性，那么我们就可以将绳子划分成块，每块长度为 $2$，要满足合法绳子的条件，每个小块都必须相等，那么如果块内的颜色是 $\{a,b\}$ 就会对 $x=a,y=b$ 以及对称情况贡献 $1$ 的代价

然后随便统计一下答案即可，枚举 $k$，需要一种支持单点 $-1/+1$ 和全局查询 min 的数据结构，用线段树做是 $O(n\log n)$ 的，用桶做是 $O(n)$ 的

28. APC001F - XOR Tree [Euclid]

题面

给定一棵 $n$ 个节点的有边权的树，边权 $a_i\le15$，每次你可以选择一条路径，并给这条路径上每一条边 $\oplus x$，问把所有边权变成 $0$ 的最小步数

$2\le n\le10^5,0\le a_i\le15$

题解

Sol

Step 1

首先把边权放到点权上

把考虑将操作树上差分一下，那么就相当于给端点分别 $\oplus x$，最后子树异或和要等于点权，我们用点权算一下最后每个点差分出来的值是什么，问题转化为每次选至多两个数 $\oplus x$，将某个数列变为全 $0$ 的方案数

Alt-Step 1

直接取数列为一个点的邻接边的边权异或和，一次操作相当于异或两个端点的权值，同样可以转化问题（其实两种方法求出来的值都是一样的）

Step 2

如果有两个相等的数，那么我们一定会把它们先异或成 $0$，反证证明，之后每一个用到这两个数的操作都可以直接把它删掉（从异或两个数变为异或一个数）

如果有 $0$，我们之后一定再也不会动它，证明同上

那么我们可以直接将每种数的个数 $\bmod2$

令 $dp_S$ 表示从开始状态变为 $S$（这里 $S$ 是一个大小为 $15$ 的集合，表示有哪些数存在）需要多少步操作

转移直接枚举一步选了什么异或上什么即可

复杂度 $O(n+2^{15}15^3)$

Alt-Step 2

开一个新图，如果我们操作了 $i$ 和 $j$ 就连一条 $(i,j)$ 的无向边，那么一个连通块内的异或和一定不变，所以最后通过对两个数异或的操作变成 $0$ 的一定是若干个异或和为 $0$ 的连通块，剩下的数单个异或成 $0$

通过两个数异或操作变为 $0$ 的需要 $size-1$ 次操作，其中 $size$ 为连通块大小

因此，问题转化为，我们要从一个 $\{1,2,\cdots,15\}$ 的子集内选出若干个不相交的子集，使得每个子集的异或和为 $0$，答案为 $n-\text{选出的集合个数}$

那么我们令 $dp_S$ 表示从 $S$ 中最多选出多少个异或和为 $0$ 的连通块，转移直接枚举子集

复杂度 $O(n+3^{15})$

29. CF578E - Walking! [Safe]

题面

一个疯子在沙地上走路。

由于他是人，所以他走路左脚和右脚交替。

由于他疯了，所以他可以在沙地上反复横跳，即他的下一脚可以在上一脚之前，我们称这种现象为“后撤步”

现在你知道这个人在沙地上留下的脚印从前往后分别是左脚 L 还是右脚 R，用字符串 $S$ 表示，由于你也疯了，所以你想知道这个人最少进行了多少次“后撤步”，并给出一种迈步的方式

保证有解。

$1\le|S|\le10^5$

题解

Sol

直接贪，我们把由后撤步分隔的每一段称为“一趟”，那么我们就是想让趟数最少

那么从 L 开始的一趟会让所有的前缀 $R-L$ 加上 $[-1,0]$，从 R 开始的一趟会让所有的前缀 $R-L$ 加上 $[0,1]$，因此趟数有下界是最大的前缀 $R-L$ 减去最小的前缀 $R-L$

事实证明，这个下界也是可以取到的，我们直接贪心地选即可，用前缀和分析一下就能发现不会有选不了的情况

我们现在将所有步划分为了若干趟，那么接下来要将它们拼起来

以起始字符和终止字符来给趟分类，只有没有 RR 和 LL 趟，且同时包含 RL 和 LR 趟的无法拼起来，而这种情况我们取包含 $n$ 的一对 RL 和 LR 来将它们变成 RR 和 LL 即可

复杂度 $O(|S|)$

30. CF1620F - Bipartite Array [Keter] ✔️

题面

给定一个 $1\sim n$ 的排列 $a$，你可以给其中的一些元素取反

对于 $i,j$，如果 $i>j$ 且 $a_i<a_j$，就在 $(i,j)$ 之间连一条边，你需要使最后连出来的图是二分图

给出构造或判断无解

$1\le n\le10^6$

题解

Sol

奇形怪状的 dp 第二期（上一期是 Bracket Insertions。）

二分图就是说可以拆成两个集合，集合内部都没有边，那么对应到序列中就是原序列可以拆成两个递增子序列

那么我们有一个朴素 dp：$dp_{i,x,y}$ 表示前 $i$ 个数，第一个子序列结尾为 $x$，第二个子序列结尾为 $y$，是否可能

我们使用 bool 状态有可能用到的 trick：把一维放到状态的值里，减小复杂度，这里由于在 $x$ 固定的情况下对后面的状态，$y$ 越小越好，因此我们可以将状态变为 $dp_{i,x}$，表示前 $i$ 个数，第一个子序列结尾为 $x$，另一个子序列结尾最小为多少

我们接着观察，发现 $x$ 和 $y$ 中至少有一个等于 $\pm a_i$，因此我们可以将状态进一步变为 $dp_{i,0/1}$，表示前 $i$ 个数，第一个子序列结尾为 $+a_i/-a_i$，另一个子序列结尾最小为多少

$O(n)$ 转移即可。

31. CF1648D - Serious Business [Euclid] ✔️

题面

一个 $3\times n$ 的矩阵，矩阵里有数 $a_{i,j}$，你要从 $(1,1)$ 向下向右走到 $(3,n)$

初始时第 $2$ 行的格子都有障碍，有 $q$ 种操作，你可以付出 $k_i$ 的代价使用第 $i$ 种操作，将 $(2,l_i)$ 到 $(2,r_i)$ 的格子中的障碍清除，你可以使用若干种操作

你最后的得分为走过的 $a_{i,j}$ 之和 - 清除障碍的代价，求最大分数

$1\le n,q\le5\times10^5$

题解

Sol

奇形怪状的 dp 第三期。

我们令 $v_a=sum1_a-sum2_{a-1}$，$w_b=sum2_b-sum3_{b-1}$，那么分别在 $a$ 处和 $b$ 处向下走（$a\le b$）的答案就是 $v_a+w_b+sum3_n+([a,b] \text{联通的代价})$

我们考虑一个奇形怪状的 dp，我们将操作按 $r$ 排序，$dp_i$ 表示当前用的 $r$ 最大的是第 $i$ 个操作，$v_a+([a,b]\text{联通的代价})$ 的最大值，那么我们有这两种转移：

$v_x-k_i\rightarrow dp_i(x\in[l_i,r_i])\\dp_j-k_i\rightarrow dp_i(l_i\le r_j+1)$

由于 $a\le b$ 很烦，所以我们不能直接通过 $dp$ 来得到答案，对于只有一次操作的答案我们可以轻松求出，多次操作的答案有如下转移

$dp_j-k_i+\max\{w[r_j+1:r_i]\}\rightarrow ans(l_i\le r_j+1)$

$\max$ 的部分可以用单调栈变成区间覆盖，这些转移就都可以放到线段树上维护了，复杂度 $O(n\log n)$

32. CF1672F2 - Checker for Array Shuffling [Euclid] ⭐

题面

给定一个数组 $a_i$，以及一个它的重排 $b_i$，定义 $a$ 与一个重排的距离 $p$ 为：通过交换 $a$ 中的任意两个数，将 $a$ 变为 $p$ 的最小次数

问对于所有 $a$ 的重排，$b$ 是不是与 $a$ 距离最大的（允许并列最大）

$1\le n\le2\times10^5,1\le a_i,b_i\le n$

题解

Sol

对于 $a$ 中相等的数，我们如果知道它们分别对应 $b$ 中的哪一个，那么从 $a_i$ 向 $b_i$ 建边，答案就是 $n-\text{环数}$

那么我们直接从 $a_i$ 向 $b_i$ 建边，最小的次数就是这张图最多能拆成多少个简单环

不难发现，对于所有重排，次数最大是 $n-\text{最大度数}$，证明留给读者作为练习。

考虑怎么判断最多拆成的环数是不是最大度数 $mx$：

首先，这张图一定由若干个环叠成的，也就是一个欧拉图

如果只有一个 $mx$，那么删掉它之后这张图必须是 dag，否则至少能拆成 $mx+1$ 个环

如果不止一个 $mx$，我们可以证明判断删掉任意一个点后是 dag 即可

设最大度数的集合为 $S$，那么假设不满足条件，这就说明存在环只覆盖了 $S$ 的一部分 $T$，对于 $S-T$ 中的点，删掉它之后一定不是 dag，对于 $T$ 中的点 $x$，由于剩下的部分也是若干个环叠成的，并且 $S-T$ 中的点的度数现在比 $T$ 中的点大 $1$，因此最多能拆成 $S-T$ 的度数个环，所以一定存在一个环不包含 $x$，所以删掉 $x$ 之后也不是 dag

因此直接删除一个最大度数的点判断是不是 dag 即可，复杂度 $O(n)$

33. CF1693D - Decinc Dividing [Keter]

题面

定义一个数列是 Decinc 的当且仅当可以从中删去一个递降子序列（可以为空），使得剩下的部分递增

给定 $1\sim n$ 的排列 $p$，求满足 $p[l:r]$ 是 Decinc 的 $(l,r)$ 数量

$1\le n\le2\times10^5$

题解

跟 Bipartite Array 太像了，所以没放 ✔️。

[做法 1]

仿照那题的思路，我们定义 $dp_{l,i,0/1}$ 表示 $[l,i]$ 内，$i$ 在上升/下降序列末尾，另一个序列的最后位置最大/最小是多少

那么有转移：

$\begin{aligned}dp_{l,i,0}&\leftarrow dp_{l,i-1,0}&(p_{i-1}<p_i)\\dp_{l,i,0}&\leftarrow p_{i-1}&(dp_{l,i-1,1}<p_i)\\dp_{l,i,1}&\leftarrow dp_{l,i-1,1}&(p_{i-1}>p_i)\\dp_{l,i,1}&\leftarrow p_{i-1}&(dp_{l,i-1,0}>p_i)\\\end{aligned}$

我们对 $i$ 扫描线，建一个关于 $l$ 的线段树，由于这个 dp 具有单调性，因此可以线段树上二分维护转移和求答案，复杂度 $O(n\log n)$

但好像可以用单调栈维护连续段？这样说不定就是 $O(n)$ 的。

[做法 2]

状态定义仍然是一样的，但我们对 $l$ 做扫描线，时刻维护每一个 $i$ 的状态

由于 $dp_{l,i,0/1}$ 之和 $dp_{l,i-1,0/1}$ 的 dp 值有关，因此我们每次 $l$ 改变，$dp_{l,i,0/1}$ 变的都是一个前缀

我们想证明直接暴力更新，遇到更新不动的就直接跳出，这样复杂度是对的

对于任意的 $l$，对于所有的 $i$，$dp_{l,i,0/1}$ 只有 $4$ 种取值，这里只证明 $dp_{l,i,0}$ 的情况，$dp_{l,i,1}$ 是对称的

我们取 $i$ 前面第一个 $p_j>p_{j+1}$ 的 $j$（如果没有的话说明这个序列递增，那么显然只有 $\infty$ 一种取值），我们说，$dp_{l,i,0}$ 的取值只有 $\{p_j,p_{j+1},\infty,-\infty\}$

证明，显然 $dp_{l,i,0}$ 不能是 $p[1:j-1]$，如果 $dp_{l,i,0}$ 是 $p[j+2:i-1]$，设其为 $p_k$，那么 $p_{k-1}$ 和 $p_{k+1}$ 一定都在上升子序列里，因此我们可以直接将 $p_k$ 放到上升子序列里

复杂度 $O(n)$

[做法 3]

一个序列是 Decinc 当且仅当不存在相对大小为 $3412$ 或 $2143$ 的子序列

证明：

如果存在，那么显然不是 Decinc 序列

如果不存在，我们要说明一定是 Decinc 序列，那么我们可以说明存在一个 LIS，使得取出这个 LIS 后剩下的部分递降

反证，如果有不在 LIS 中的 $i,j$，满足 $i<j$ 且 $a_i<a_j$

如果 $i$ 大于 LIS 中 $i$ 的二级前驱的值（前驱的前驱），那么我们可以直接将 $i$ 的前驱删掉将 $i$ 放入 LIS，长度不变，小于 LIS 后面两个也是一样

因此我们只用考虑 $i$ 和 $j$ 大于后面两个或者小于前面两个的情况，分别在这里枚举了（黑点是 LIS，星星是 $i,j$）：

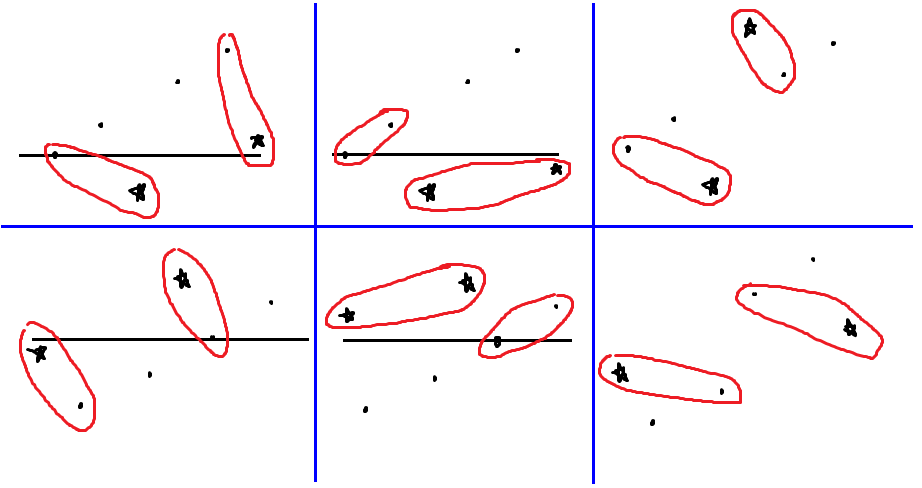
不管怎么样，我们都可以选出红圈框住的四个数，形成 3412 或 2143 的形态，因此可以得证

然后好像用 ds 维护一下就可以了

复杂度 $O(n\log n)$

34. CF1616H - Keep XOR Low [Euclid]

题面

给定 $a_1,a_2,\cdots,a_n$ 以及 $x$，求有多少选出一个非空子集的方法，使得这个子集中任意两个数异或值 $\ge x$

$1\le n\le1.5\times10^5,0\le x,a_i<2^{30}$

题解

Sol

我们从高到低考虑每一位，建出 trie 树

如果当前的最大异或已经小于 $x$，那么答案可以直接用 $2$ 的次方算出来，如果 $x$ 的这一位为 $0$，那么选的数这一位必须都相等，左右两个子树选一个进即可，如果 $x$ 的这一位为 $1$，那么就需要拆成两个节点

但我们可以继续对两个节点的情况搜索，具体地，我们设 $f(i)$ 表示当前在 trie 树上的节点 $i$，在子树中选异或不大于 $x$ 的后 $dep$ 位的选法数，$g(i,j)$ 为当前在 trie 树上的两个节点 $i,j$，要求这两个子树之间的异或不大于 $x$ 的后 $dep$ 位的选法数，那么我们有大致的关系式（$x(d)$ 表示 $x$ 的第 $d$ 位）

$\begin{aligned}f(i)&\leftarrow f(lc_i),f(rc_i),&&x(d)=0\\f(i)&\leftarrow g(lc_i,rc_i),&&x(d)=1\\g(i,j)&\leftarrow g(lc_i,lc_j),g(rc_i,rc_j)&&x(d)=0\\g(i,j)&\leftarrow g(lc_i,rc_j),g(rc_i,lc_j)&&x(d)=1\\\end{aligned}$

箭头表示左边的状态可以由右边的状态进行 $O(1)$ 计算得出

我们直接搜索复杂度就是对的，考虑 $g$ 的数量，因为我们的搜索过程只会搜索到异或等于 $x$ 的前几位的点对，于是每一层的节点数都是 $O(n)$ 的，整体也就是 $O(n\log a_i)$

35. CF1721F - Matching Reduction [Keter]

题面

给定一个二分图，左部点 $n_1$ 个，右部点 $n_2$ 个，$m$ 条边

有 $q$ 次询问，每次询问是 1 或 2 中的一种：

1：从二分图中删除最少的点，使得最大匹配恰好减小 $1$，输出删的点以及删完之后任意一个最大匹配的边的编号之和

2：这类询问只会在 1 询问的下一个后面出现，你需要输出你在上次 1 操作输出的最大匹配的所有边

强制在线。

$1\le n_1,n_2,m,q\le2\times10^5$，最多有 $3$ 个 2 询问

题解

Sol

完全不会二分图题。

考虑最大匹配等于最小点覆盖，那么我们就是要让最小点覆盖减小 1，这样我们删除点覆盖中任意一个点即可，与这条边相连的点也被删除了，因此剩下的部分是一个合法的点覆盖

而如果剩下的部分的最小点覆盖小于原来的最小点覆盖 $-1$，那么我们将新的点覆盖加上删掉的点就得到一个比原来更优的点覆盖，因此矛盾，所以删除一个最小点覆盖中的点一定对应着最小点覆盖大小恰好 $-1$，也即最大匹配 $-1$

我们得出最大匹配方案和最小点覆盖方案，之后每次删一个点，这是好维护的

[附件]

最小割求方案：

好像在残量网络上直接从 $S$ 开始搜，走剩余流量不为 0 的边（包括反向边），然后搜出包含 $S$ 的连通块后直接取连通块向外连的边所有边为割边集就是对的

ex：在残量网络上对没流完的边跑 tarjan，缩点成 dag，在这个 dag 上取任意一个边集，使得这个边集不存在两条边满足从一条边能走没流完的边走到另一条边，那么这个边集就是一个最小割

36. CF1687D - Cute Number [Euclid]

题面

定义 $g(x)$ 为 $\le x$ 的最大完全平方数，$f(x)$ 为 $>x$ 的最小完全平方数

给定 $a_1,a_2,\cdots,a_n$，求一个最小的 $k$ 使得 $a_i+k-g(a_i+k)<f(a_i+k)-(a_i+k)$ 对任意 $i$ 成立

$1\le n\le10^6,1\le a_1\le a_2\le\cdots\le a_n\le2\times10^6$

题解

Sol

令 $A$ 为值域

$x-g(x)<f(x)-x$ 的从 $1$ 开始：满足 $2$ 个，不满足 $1$ 个，满足 $3$ 个，不满足 $2$ 个，以此类推

那么在第 $2A$ 个连续段左右一定是一个连续满足 $A$ 个的，因此答案有了一个上界

那我们枚举 $a_1+k$ 在哪个满足段，设这个满足段的长度为 $x$，$k$ 的范围就被限定在了一个区间内，我们先假设 $a_1$ 加到 $k_{\min}$，算 $k$ 增加的范围

之后的每一段长度都 $\ge x-1$，因此每个数要么是随着 $k$ 在这个区间内增加，从满足变为不满足，要么是从不满足变为满足（只会变一次），每个数都对 $k$ 有一个限定的范围，限制 $k\ge r_i$ 或者 $k\le r_i$

那么我们只要能求出每个数的限制的交，就能判断有没有合法的 $k$

考虑每一段内只有第一个数（满足段）或者最后一个（不满足段）有用，所以我们可以 $O(\text{段数})$ 来求所有限制的交，而如果当前满足段的长度为 $x$，那么之后的段长度都 $\ge x-1$，因此有数的段最多 $\frac Ax$ 个，我们只需要枚举这么多就可以了

复杂度是 $O(\sum\frac Ax)=O(A\ln A)$

37. CF1712F - Triameter [Keter] ✨

题面

给定一棵 $n$ 个节点的树，边权都为 $1$，$q$ 次询问，每次询问给出 $x$，表示在叶子之间（定义为度数为 $1$ 的点）两两连一条边权为 $x$ 的无向边，之后询问任意两点间的最短路的最大值，询问之间独立

$3\le n\le10^6,1\le q\le10,1\le x_i\le n$

题解

Sol

如果两点之间最短路经过新加的边，那么只会经过一次，证明显然

我们令 $a_u$ 表示 $u$ 在只走树边的情况下，到最近的叶子的距离

那么 $dis(u,v)=\min\{a_u+a_v+x,dep_u+dep_v-2dep_{\text{lca}(u,v)}\}$，我们要求对于所有 $u,v$ 这个东西的最大值

由于这个深度看起来很讨厌，所以我们考虑长链剖分来处理它，这里我们有两种设状态的方式

$f_{u,i}$ 表示 $u$ 子树中 $dep_v=i$ 的 $\max a_v$
$f_{u,i}$ 表示 $u$ 子树中 $a_v=i$ 的 $\max dep_v$

我觉得正常人都只会想到第一种吧！！！但是神说，你应该选第二种状态。

神说，第二种状态有性质，$f_{u,i}\ge f_{u,i+1}$，证明考虑如下几件事：

任意两个相邻点的 $a$ 之差不超过 $1$
$u$ 的 $a$ 为 $a_u$，叶子的 $a$ 为 $0$
因此 $u$ 到叶子的路径最深的 $a_u$ 及它向下的部分的 $a$ 值一定包含了 $[0,a_u]$ 中的所有数，而 $u$ 子树中的点 $dep$ 都 $\ge dep_u$，因此 $f_{u,i}\ge f_{u,j}(i<j)$

接下来考虑统计答案：

我们要求 $\min\{x+a_u+a_v,dep_u+dep_v-2dep_{\text{lca}(u,v)}\}$ 最大

神说，你可以采用每次看当前值是否 $\ge ans+1$，如果是那么给 $ans$ 加 $1$

我们维护了 $f_{u,i}$，所以我们首先考虑 $x+a_u+a_v\ge ans+1$，由于这是长剖，所以我们可以枚举一个 $a$，不妨设剩下的是 $a_v$，那么 $a_v$ 需要满足 $a_v\ge ans+1-x-a_u$，我们发现，直接取 $dep_v=f_{u,ans+1-x-a_u}$ 就是最优的（这里可能出现负数下标的情况，和 $0$ 取 max 即可），因为 $dep_u+dep_v-2dep_{\text{lca}(u,v)}$ 显然 $dep_v$ 越大越有可能 $\ge ans+1$，因此直接将这个值代入即可

复杂度是长剖经典复杂度分析，由于我们对 $q$ 个询问算答案，复杂度 $O(nq)$

据说这题还可以做 $n,q\le10^6$，不会，先咕着。

38. CF1621G - Weighted Increasing Subsequences [Euclid] ⭐

题面

给定 $a_1,a_2,\cdots,a_n$，对于它的一个上升子序列 $a_{i_1},a_{i_2},\cdots,a_{i_k}$，我们定义它的权值为满足存在 $x$ 使 $i_k<x\le n$ 且 $a_{i_j}<a_x$ 的 $j$

对于所有上升子序列求权值和，对 $10^9+7$ 取模

$1\le n\le2\times10^5$

题解

Sol

显然可以把每一位的权值贡献拆开来考虑，那么我们就要求每一个位置在多少个上升子序列里有贡献

考虑一个 $a_i$ 什么时候会产生贡献，经过一些观察，我们发现如果找到最后一个满足 $a_i<a_x$ 的 $x$，那么 $a_i$ 会产生贡献当且仅当 $a_x$ 不在上升子序列中，可以容斥一下变为求包含 $a_i,a_x$ 的上升子序列个数

有一些显然的事情：

$a_x$ 是后缀最大值
包含 $a_i,a_x$ 的上升子序列在 $i$ 之前的方案数是 $pre_i$，以 $i$ 结尾上升子序列的数量，在 $x$ 后面的方案数是 $1$，因此我们只用考虑 $[i,x)$ 的部分，而这部分所有元素都在 $[a_i,a_x)$ 之内

因此，如果我们用后缀最大值给值域分段（即对于后缀最大值 $b_1,b_2,\cdots,b_k$，将 $[b_{i-1},b_i)$ 分为一段），这样每个非后缀最大值的数都会被分进恰好一段（后缀最大值我们直接扔掉），那么我们只用在每一段内求以每个数为起点的上升子序列个数就是每个数的 $[i,x)$ 部分的方案，具体原理大概画个图就看出来了，但是 md 插入图片很麻烦，所以我懒得画了。

复杂度 $O(n\log n)$

39. CF1610H - Squid Game [Keter] ✔️

题面

给定一棵 $n$ 个点的树，这上面有 $m$ 条链 $(x_i,y_i)$

你可以进行若干次操作，每次操作选择一个点 $v$，对于所有链 $(x_i,y_i)$，如果链上距离 $v$ 最近的点不是 $x_i$ 或 $y_i$ 就将这个链删去

问最少多少次操作能够将所有链删去，或判断无解

$1\le n,m\le3\times10^5$

题解

Sol

考虑操作一个点 $v$ 之后，我们以 $v$ 为根，任何不是祖孙链的链都会被删去，并且祖孙链一定都没事

那么我们枚举第一步操作，之后只剩点 $v$ 了，我们有一种贪心：每次找到深度浅的节点尽量深的链，选条链第二浅的点，这样一定不会使答案变得更劣

我们如果用树状数组维护这件事情就是 $O(n^2\log n)$ 的

但其实我们不用枚举第一步操作，我们有一个结论：直接以 $1$ 为根，忽略所有非祖孙链求答案，如果此时存在非子孙链未被删除，那么操作 $1$，给答案 $+1$

证明的话考虑非祖孙链 $(x_i,y_i)$，如果它还没有被删除说明选了的点一定都在 $x_i$ 和 $y_i$ 的子树中，而由于我们的构造方式保证构造出来的一定是“尽量浅”的解，所以再调整肯定不能使 $(x_i,y_i)$ 被删除（这部分好像不太严谨），必须额外用一次操作将其删除

那么我们直接树状数组求解即可，复杂度 $O(n\log n)$