rand

[TOC]

1. CF1004F - Sonya and Bitwise OR

题面

给定 $n,m,x$，以及一个长为 $n$ 的数组 $a_1,a_2,\cdots,a_n$

有 $m$ 次操作，操作为下面两种的一种：

1. $1 i y$，表示将 $a_i$ 赋值为 $y$
2. $2 l r$，求有多少有序对 $(x,y)$ 满足 $l\le x\le y\le r$，并且 $a_l|a_{l+1}|\cdots|a_r\ge x$，其中 $|$ 代表按位或

$1\le n,m\le10^5,0\le x<2^{20}$，保证任意时刻 $0\le a_i<2^{20}$

题解

考虑使用线段树维护每个区间的答案，那么在合并时需要我们求出跨过区间中点的满足条件的答案个数

在以某一个下标开始的区间或最多有 $\log a_i$ 种，证明显然

因此，我们可以直接维护前缀的或段以及后缀的或段，然后合并的时候拼接即可

复杂度 $O(n\log^2n)$

2. CF1089K - King Kog’s Reception

题面

现在有一些人，每个人有一个来的时间 $t$ 和办事需要的时间 $d$，这些人会按照来的时间的顺序办事，由于两个人并不能同时办事，所以后来的人会等先来的人办完事再开始办事

有 $q$ 次操作，每次操作是如下三种中的一种：

1. + $t$ $d$，表示新增一个在 $t$ 时刻来并且办事时长为 $d$ 的人
2. - $x$，表示删除第 $x$ 次操作增加的人
3. ? $t$，表示如果此时 $t$ 时刻来了一个人，那么他需要等多长时间才能开始办事

$1\le q\le3\times10^5$

题解

假设我们已经将所有人按照时间排序，那么一个人 $x$ 办上事的时间是 $\max(t_i+d_i+d_{i+1}+\cdots+d_{x-1})(1\le i\le x)$，化为 $t_i+sum_{x-1}-sum_{i-1}$，用平衡树/线段树维护即可，复杂度 $O(n\log n)$

3. CF1063E - Lasers and Mirrors

题面

你有一个 $n\times n$ 的棋盘，现在对于每一个 $i$，第 $i$ 列上方射入了颜色为 $i$ 的光线，给定数列 $a_i$，表示第 $i$ 列下方放置了颜色为 $i$ 的接收器

你现在要在这个棋盘中的一些格子放置倾斜 45° 的平面镜，用 \ 与 / 表示，使得尽可能多的接收器接收到对应颜色的光线

$1\le n\le1000$

题解

如果 $a_i=i$，那么答案一定是 $n$，否则答案为 $n-1$

证明：考虑第一个有镜子的行，必定会淘汰掉至少一个光线，因此答案最多为 $n-1$，否则我们可以如下构造出 $n-1$ 的解

情况 1：考虑如果当前我们有 $m$ 列，第 $i$ 列没有光射入，第 $j$ 列没有接收器，$i\neq j$，且如果将除 $i,j$ 外的列的光与接收器颜色连边，那么所有颜色形成一条链

当 $m=2$ 时直接反射即可

否则我们用第一行将可以第 $i$ 列的接收器所对应的光反射过来，设其在列 $x$，那么问题转化为 $m-1$ 列，第 $x$ 列没有射入光，第 $j$ 列没有接收器的情况，那么我们就在 $m-1$ 步内完成了这一类情况

情况 2：考虑如果当前有 $m$ 列，这 $m$ 列的光与发射器的排列成一个大环，以及一个在最右侧的空余列（既没有光射入也没有接收器）

我们可以将第 $m$ 列的光反射到空余列，并转化为有 $m+1$ 列，第 $m$ 列没有光射入，第 $m+1$ 列没有接收器的情况，用 $m$ 行解决即可，这样我们将这 $m$ 行的第一行与将第 $m$ 行反射到第 $m+1$ 行合并，就可以得到这个问题 $m$ 行的解

现在考虑如何造出这个空余行，由于我们希望空余行在最右侧，因此我们扔掉第 $n$ 列接收器的颜色的光线，接着对排列的每一个环考虑：

1. 该环包括被扔掉的光线，那么可以转化为情况 1，消耗 环长-1 行
2. 该环不包括被扔掉的光线，那么可以转化为情况 2，消耗 环长 行

再加上最开始扔掉光线的行，一共 $n$ 行解决

4. CF1063D - Candies for Children

题面

给定 $n,l,r,k$，现在有 $n$ 个小朋友顺次顺时针排成一圈，有一个装有 $k$ 个糖果的盒子，从第 $l$ 个小朋友开始顺时针传，每个小朋友有一个属性 $k_i(k_i\in\{1,2\})$，表示每当盒子传到这个小朋友时她会拿走 $k_i$ 块糖（如果剩下的糖果数不足 $k_i$ 则全部拿走），已知第 $r$ 个小朋友拿走了最后一块糖，问最多可能有多少小朋友的 $k_i=2$

$1\le n,k\le10^{11},1\le l,r\le n$

题解

设有 $x$ 个小朋友的 $k_i=2$，那么：

$$\left\{ \begin{aligned} k\bmod(n+x)\ge id\\ k\bmod(n+x)\ge x-(n-id)+id\\ k\bmod(n+x)\le 2id-1\\ \end{aligned} \right.$$

整理后整除分块解不等式即可，复杂度 $O(\sqrt n)$

5. CF682E - Alyona and Triangles

题面

给定 $n$ 个整点，保证其中任意三点组成的三角形面积不超过 $S$，要求构造一个整点三角形，使得其包含所有的 $n$ 个点，且面积不超过 $4S$

$1\le n\le5000,1\le S\le10^{18}$

题解

结论：任选一个面积最大的由这 $n$ 个点组成的三角形，分别过其三个顶点作对边平行线组成的三角形即为答案

证明：如果有点在三角形外，如图（面积最大的三角形为紫色三角形，答案三角形为直线围出的三角形）：

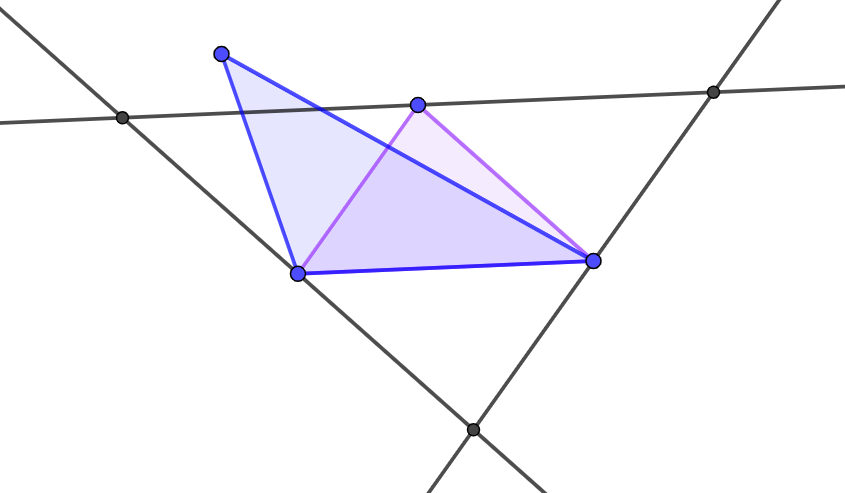
那么蓝色三角形的面积一定大于紫色三角形，矛盾

现在我们要找出这 $n$ 个点组成的最大的三角形

不难发现这个三角形端点一定在凸包上，我们不妨假设三角形顶点分别是 $A,B,C$（顺时针顺序），那么我们先枚举 $A$，接下来随着 $B$ 顺时针移动时，$C$ 的最优取值一定也顺时针移动，维护一下即可，复杂度 $O(n^2)$

6. CF652F - Ants on a Circle

题面

在一个长度为 $m$ 的圈（逆时针 $1\sim m$ 编号）上有 $n$ 只蚂蚁，每只蚂蚁有一个方向（顺时针或逆时针）与一个起始位置，蚂蚁会以每单位时间 $1$ 单位距离的速度爬行，当两只蚂蚁相遇时她们会分别调转方向继续爬行，问 $t$ 单位时间后每只蚂蚁的位置

$2\le n\le3\times10^5,2\le m\le10^9,0\le t\le10^{18}$

题解

考虑蚂蚁位置的相对顺序一定不变，所以任意时刻我们只要确定其中一只蚂蚁的位置便能确定其他所有蚂蚁的位置

我们可以把蚂蚁相遇看做对穿互换编号来计算最终位置

考虑经过 $t$ 单位时间相当于经过了 $\lfloor\frac tm\rfloor$ 个 $m$ 单位时间以及一个 $t\bmod m$ 单位时间

经过 $m$ 单位时间位置集合一定和原来一样，因此我们可以算出编号旋转了多少位直接乘 $\lfloor\frac tm\rfloor$

观察得一个逆时针的蚂蚁每次对穿编号一定 $+1$，因此可以枚举计算相遇多少次算出偏移量，然后直接计算即可，复杂度 $O(n)$

7. CF625D - Finals in Arithmetic

题面

给定一个正整数 $n$，要求构造一个正整数 $a$ 使得将 $a$ 所有位翻转顺序得到的数与 $a$ 的和为 $n$

$1\le n\le10^{100000}$

题解

考虑确定第一位是否是进位后可以直接由外往里推出，直接 $O(\lg n)$ 解决

8. CF605D - Board Game

题面

你当前在 $(0,0)$，你有 $n$ 种操作，第 $i$ 种操作有四个属性 $a_i,b_i,c_i,d_i$，如果你当前在 $(x,y)$，满足 $x\ge a_i,y\ge b_i$，那么你可以选择移动到 $(c_i,d_i)$，问你最少要多少次操作才能使用第 $n$ 个操作，无解则输出 $-1$

$1\le n\le10^5$

题解

考虑暴力 bfs，每次暴力枚举哪些操作可以在执行完当前操作后执行，这样复杂度无法接受

考虑优化，每个操作只需要被它对应的最优解更新，并且在被更新后便不需要再在更新其他操作时枚举该操作，因此我们可以转化为，每次要找出所有 $a_i\le x,b_i\le y$ 的操作，并将它们从全集中删除，可以用 树状数组+set 维护，复杂度 $O(n\log^2n)$

9. CF576D - Flights for Regular Customers

题面

有一张 $n$ 个点 $m$ 条边有向图，可能有自环，每条边有一个权值 $x_i$，表示你在走这条边之前必须先走了至少 $x_i$ 条边，求 $1$ 到 $n$ 的最小步数

$1\le n,m\le150,x_i\le10^9$

题解

考虑最优解走的边数可能很大，所以我们用矩乘维护是否可行

我们将边按 $x_i$ 从小到大排序，每次到枚举到一条边时先计算出 $x_i$ 步的联通情况，然后将邻接矩阵中改边设为 1，如果这样能到达，那么在 $x_{i-1}$ 与 $x_i$ 内二分

这样复杂度是 $O(mn^3\log W+n^3\log^2W)$，使用 bitset 优化可到 $O(\frac{mn^3\log W+n^3\log^2W}{\omega})$

10. CF534E - Berland Local Positioning System

题面

有数轴上有一条公交车线路，其中从左到右第 $i$ 站的坐标为 $a_i$，有一辆公交车，会沿着 $1\rightarrow2\rightarrow\cdots\rightarrow n\rightarrow n-1\rightarrow\cdots\rightarrow1\rightarrow\cdots$ 的线路运行，现在这辆公交车在某一个时间段内，起始在某一个车站，结束在某一个车站，途中一共经过了 $m$ 次车站，现在升序给出这 $m$ 个车站的编号，问这辆车在这个时间段内经过了多少的距离，如果不能确定或不可能则输出 $-1$

$1\le n\le2\times10^5,1\le m\le4\times10^5$

题解

直接模拟即可。

枚举起始车站以及方向（可以将环倍长避免讨论），那么可以动态维护从起始车站开始的 $m$ 个车站的集合，然后与给出集合比对（可以维护有多少车站出现次数与目标集合不同）

复杂度 $O(n+m)$

11. CF513D1 - Constrained Tree

题面

有 $c$ 个限制 $a_i,b_i,typ_i$，要求构造一棵 $n$ 个点的二叉树，使得其前序遍历为 $1,2,\cdots,n$，且对于每个限制 $a_i,b_i,typ_i$，其中 $typ_i$ 为 LEFT 或 RIGHT，表示 $b_i$ 需要在 $a_i$ 对应的子树内

$1\le n\le100,1\le c\le50$

题解

令 $dp_{i,x}$ 表示编号为 $i$ 的点的子树有 $x$ 个点是否可能，枚举左子树大小记录转移点转移即可，复杂度 $O(n^2c)$

12. CF452F - Permutation

题面

给定长为 $n$ 的排列 $p$，判断是否存在 $x,y,z$，满足 $1\le x<y<z\le n,p_y=\frac{p_x+p_z}2$

$1\le n\le3\times10^5$

题解

考虑求出 $id_i$，表示 $i$ 在排列中出现的位置，那么问题相当于我们要找到三个下标 $x,y,z$，使得 $x,z$ 关于 $y$ 对称且 $id_x,id_y,id_z$ 递增或递降

对于一个 $y$，如果我们将小于 $id_x$ 的数视为 0，将大于 $id_x$ 的数视为 1，那么如果以 $y$ 为中心的最长串是回文串，那么无法取出，否则可以取出，每次单点修改哈希判断即可

复杂度 $O(n\log n)$

13. CF995E - Number Clicker

题面

给定 $u,v,p$，你每次可以在模 $p$ 意义下进行三种操作的一种：将 $u$ 加 $1$，将 $u$ 减 $1$，将 $u$ 取倒数，要求构造一个长度不超过 $200$ 的操作序列，使得依次执行后 $u$ 变为 $v$

$0\le u,v\le p-1,3\le p\le10^9+9$，$p$ 为质数

题解

考虑这个操作形成的图看起来很随机，于是我们可以考虑乱搞

不难发现操作是可逆的

做法 1

随机生成 $x$ 个长度为 $100$ 的从 $u$ 开始的路径，将它们存到一个 set 中，然后再随机生成从 $v$ 开始的路径，直到路径的结束点在集合内为止，根据生日悖论，期望运行时间是 $O(200\cdot x\log p+200\cdot\frac px\log p)$，取 $x=\sqrt p$ 最优

做法 2

直接双向 bfs，据 CF editorial 不会访问超过 $10^7$ 个点

14. CF983E - NN country

题面

给定一棵 $n$ 个点的树，这棵树上有 $m$ 条路径，你每一步可以选择一条经过你所在的点的路径，并走到这条路径上的任意一个点

$q$ 次询问，每次询问从 $u$ 到 $v$ 最少要多少步，如果不能到达则输出 $-1$

$1\le n,m,q\le2\times10^5$

题解

做法 1

贪心是显然的：每次直接走到在 $u\rightarrow v$ 方向上最远的点

倍增，维护 $to[i][j]$ 表示从 $i$ 向上走 $2^j$ 步走到的最浅的祖先，这样就能处理出任何一个向上的链最少需要跳多少步

但询问的链不一定是向上的链，容易想到两边分别往上跳，最后再合并起来

具体地，我们将 $u$ 和 $v$ 向上跳，跳到最后一个还在 LCA 以下的点，然后我们要判断是否有一条链覆盖 $u,v$ 这两个点

对于这个问题，我们按 $u$ 的 dfn 离线，然后 dfs 求解，每次启发式合并求出有一个端点在 $u$ 子树内的链的 $v$ 的集合，将这个集合按 dfn 排序，然后查询是否有元素在 $v$ 的子树内即可，用 set 维护

复杂度 $O(n\log^2n)$

做法 2

然后我们要判断是否有一条链覆盖 $u,v$ 这两个点

考虑这个问题就是 dfn 上的二维数点，离线树状数组，复杂度 $O(n\log n)$

15. CF958C3 - Encryption (hard)

题面

给定一个长度为 $n$ 的序列 $a$，要求将其拆为 $k$ 个非空连续段，使得这些段内数和对 $p$ 取模的和最小，求最小和

$1\le n\le5\times10^5,2\le k,p\le100$

题解

挺奇妙的一个题，看了眼题解想出来了。。

考虑朴素 dp：$dp[i][j]$ 表示前 $i$ 个数分为 $j$ 段的方案，那么转移为 $dp[i][j]=\min(dp[k][j-1]+((sum_k-sum_i)\bmod p))$，这样复杂度是 $O(n^2k)$ 的，无法通过

不难发现 $dp[i][j]\equiv sum_i\pmod p$，而 $0\le(sum_k-sum_i)\bmod p<p$，因此从 $dp[k][j-1]$ 转移来的值会是大于等于 $dp[k][j-1]$ 的第一个模 $p$ 同余于 $sum_i$ 的数，不难发现直接从最大的 $dp[k][j-1]$ 转移过来最优，因此直接 $O(1)$ 转移，复杂度 $O(nk)$

16. CF924D - Contact ATC

题面

有 $n$ 坨飞机，第 $i$ 坨飞机的坐标为 $x_i$，正方向上的速度是 $v_i$（若为负数则表示向负方向运动），且保证每坨飞机都是朝原点方向运动（$x_iv_i<0$）

给定一个数 $w$，保证任何一个 $v$ 的绝对值都大于 $w$，对于一个无序飞机对 $(i,j)$，如果你可以选择一个 $[-w,w]$ 内的实数使得将 $i$ 和 $j$ 的速度加上这个值后他们同时到达原点，那么我们称它为好的

问有多少好的无序飞机对，$1\le n\le10^5$

题解

推式子

当 $v_iv_j<0$ 时：如果 $i$ 和 $j$ 满足 $\frac{x_i}{v_i-w}\ge\frac{x_j}{v_j-w}$，且 $\frac{x_i}{v_i+w}\le\frac{x_j}{v_j+w}$

当 $v_iv_j>0$ 时：如果 $i$ 和 $j$ 满足 $\frac{x_i}{v_i-w}\le\frac{x_j}{v_j-w}$，且 $\frac{x_i}{v_i+w}\ge\frac{x_j}{v_j+w}$

直接二维数点即可，复杂度 $O(n\log n)$

17. CF913F - Strongly Connected Chess Tournament

题面

有 $n$ 个人要进行一次竞赛，竞赛分若干轮，每轮按如下方式进行：

1. 两两进行一次对决，没有平局
2. 从胜者向负者连边，建出一张竞赛图
3. 对于每个强联通分量递归进行同样的一轮比赛

已知第 $i$ 个人赢第 $j$ 个人的概率是 $p$，求比赛的期望对决数，对 $998244353$ 取模

$2\le n\le2000$

题解

dp。

对于集合 $S$，我们令 $f(S)$ 表示集合 $S$ 的期望轮数，则我们枚举哈密顿路上的最后一个强联通分量的集合 $T$，那么我们得到

$$f(S)=\sum_{T\subseteq S}(f(T)+f(S-T)+\frac12|T|(|T|-1)+|T|(|S|-|T|))t(T)edgeW(S-T,T)\\$$

其中，$t(T)$ 代表 $T$ 集合内部的边形成一个强联通分量的概率，$edgeW(S,T)$ 表示 $S$ 集合内的点与 $T$ 集合内的点之间的边全部指向 $T$ 集合内的点的概率

考虑如果 $|T|$ 确定，那么 $t(T)$ 显然是可以确定的，当 $|T|=x$ 时，我们记 $t^\prime(x)$ 为对于所有满足条件的 $T$ 的 $t(T)$ 之和。采用容斥，然后枚举最后一个，写出表达式为：

$$t^\prime(x)=1-\sum_{y=1}^{x-1}t^\prime(y)\sum_{|S|=y,|S|\in\{1,2,\cdots,x\}}edgeW(\{1,2,\cdots,x\}-S,S)\\$$

考虑 $f$ 的值也只与集合大小有关，并且在 $t^\prime$ 与 $f$ 的转移式中，当集合的大小确定时 $edgeW$ 前面的系数均不变，只有 $edgeW$ 的值发生变化，因此可以通过分配率将它们结合在一起，这样转移式便脱离了枚举集合。我们令 $f^\prime$ 为集合大小为 $x$ 时所有满足条件的 $f(S)$ 之和，可以得到 $t^\prime$ 与 $f^\prime$ 的转移式：

$$f^\prime(x)=\sum_{y=1}^{x}(f^\prime(y)+f^\prime(x-y)+\frac12y(y-1)+y(x-y))t^\prime(y)edgeW^\prime(x,y)\\ t^\prime(x)=1-\sum_{y=1}^{x-1}t^\prime(y)edgeW^\prime(x,y)$$

其中 $edgeW^\prime(x,y)$ 表示有 $x$ 个点，对于所有满足 $|T|=y$ 的集合 $T$，$edgeW(\{1,2,\cdots,x\}-T,T)$ 之和

考虑这个式子会涉及到 $f^\prime(x)$ 转移到自己，因此需要移项，得到：

$$f^\prime(x)=\frac{\left(\sum_{y=1}^{x}(f^\prime(y)+f^\prime(x-y)+\frac12y(y-1)+y(x-y))t^\prime(y)edgeW^\prime(x,y)\right)}{1-t^\prime(x)edgeW^\prime(x,x)}$$

那么接下来我们需要求出 $edgeW^\prime(x,y)$，考虑其等于：

$$\begin{aligned} edgeW^\prime(x,y)&=\sum_{T\in\{1,2,\cdots,x\},|T|=y}p^{\sum_{i\in T}i-rk_i}(1-p)^{\sum_{i\in T}(x-i)-(y-rk_i)}\\ &=\sum_{T\in\{1,2,\cdots,x\},|T|=y}p^{-\frac12y(y+1)}(1-p)^{y(x-y)+\frac12y(y+1)}\left(\frac p{1-p}\right)^{\sum_{i\in T}i}\\ &=p^{-\frac12y(y+1)}(1-p)^{y(x-y)+\frac12y(y+1)}\sum_{T}\left(\frac p{1-p}\right)^{\sum_{i\in T}i} \end{aligned}$$

我们令 $h(x,y)=\sum_{T=\{1,2,\cdots,x\},|T|=y}\left(\frac p{1-p}\right)^{\sum_{i\in T}i}$ ，则 $h(x,y)=\left(\frac p{1-p}\right)^{\sum_T\sum_{i\in T}i}$，不难得到转移式 $h(x,y)=h(x-1,y)+h(x-1,y-1)\left(\frac p{1-p}\right)^x$

至此，所有式子都可以 $O(n^2)$ 计算，因此可以解决该问题

18. CF860E - Arkady and Nobody-men

题面

给定一棵 $n$ 个点的树，定义 $r(a,b)$ （其中 $b$ 为 $a$ 的祖先）为 $b$ 子树（不含 $b$）中深度小于等于 $a$ 的数的个数，令 $z_a=\sum_{b是a的祖先}r(a,b)$，求每个点的 $z$

$1\le n\le5\times10^5$

题解

考虑按深度添加节点，那么我们求一个点的 $z$ 就相当于求这个点到根的链上的子树大小和，树剖维护即可，复杂度 $O(n\log^2n)$，卡常可过

19. CF235C - Cyclical Quest

题面

给定一个串 $s$ 以及若干个串 $t$，对于每个 $t$，求有多少 $s$ 的子串与 $t$ 循环同构

$|s|\le10^6,\sum|t|\le10^6$

题解

对 $s$ 建 SAM，然后在 $t$ 上匹配即可

20. CF204D - Little Elephant and Retro Strings

题面

如果一个由 B 和 W 组成的串内，存在两个不相交子串 $s_1,s_2$，使得 $|s_1|=|s_2|=k$，且 $s_1$ 内所有字符均为 B，$s_2$ 内所有字符均为 W，则称这个串是伟大而又神圣的

给定一个由 B，X，W 组成的长为 $n$ 的串，你需要将每个 X 替换为 B 或 W，使得这个串是伟大而又神圣的，求有多少种方案，对 $10^9+7$ 取模，$1\le k\le n\le10^6$

题解

对于每个伟大而又神圣的串，我们放在第一个全 B 的长为 $k$ 的子串处统计

枚举全 B 串的位置 $[x:x+k-1]$，那么 $[1:k-1]$ 内不能有长为 $k$ 的全 B 串，$[x+k:n]$ 内必有一个长为 $k$ 的全 W 串，这两个都可以通过 dp 求得，复杂度 $O(n)$

21. CF176D - Hyper String

题面

给定若干个小写字母串 $t_1,t_2,\cdots,t_n$，再给定一个长为 $m$ 的序列 $id_1,id_2,\cdots,id_m$，定义 $T=t_{id_1}t_{id_2}t_{id_3}\cdots t_{id_m}$，给定 $S$，求 $S$ 与 $T$ 的 lcs 长度

$1\le n,m,|S|\le2000,\sum|t_i|\le10^6,\forall |t_i|>0$

题解

令 $dp[i][j]$ 表示 $S[1:i]$ 在 $T$ 中能匹配完的最早位置，则 $dp[i][j]=\min(dp[i-1][j],nxt(dp[i-1][j-1],S[i]))$，$O(n^2)$ 转移即可