CF1054

不要弃赛！！！！！11

A

题面

Masha 在 $x$ 层，她要去第 $y$ 层，她可以乘电梯或者走楼梯，电梯现在在 $z$ 层，并且关着门，走楼梯一层需要 $t_1$ 的时间，乘电梯一层需要 $t_2$ 的时间，电梯开关门需要 $t_3$ 的时间，问楼梯和电梯哪个更优

题解

直接模拟即可。

B

题面

一开始有一个空的数组，执行 $n$ 次操作，每次操作将现在数组中的 mex 添加到后面，现在给出 $a$，问能不能通过这种方式生成，若不能请输出第一个出错的下标，$1\le n\le10^5$

题解

通过这种方式生成的数组一定是 $0,1,\cdots,n-1$，所以找到第一个 $a_i\neq i$ 的下标即可

C

题面

有 $n$ 个小朋友排成一列，每个小朋友有若干糖果，且 $1\le \text{糖果数}\le n$，现在给出 $l_i,r_i$，分别表示第 $i$ 个小朋友左边有多少个糖果数大于他的与第 $i$ 个小朋友右边有多少个糖果数大于他的，请判断是否可能形成这种局面，如果可能，请构造一种每个小朋友糖果数量的方案数，$1\le n\le1000$

题解

判一下 $l_i>i-1$ 与 $r_i>n-i$ 的情况，显然每个小朋友糖果数量的排名就是 $l_i+r_i+1$，判断一下个数是否合法即可

D

题面

有一个长度为 $n$ 的序列 $a_i$，其中每个元素都在 $[0,2^k-1]$ 之间，你可以将其中若干个元素异或上 $2^k-1$，要求使得最后异或和不为 $0$ 的尽量多，求最多为多少，$1\le n\le200000,1\le k\le30$

题解

考虑求出前缀和，则每次操作就是选择一个后缀将前缀和都取反，那么可以视作为选择一个前缀和将其取反

于是问题变成，你有 $n+1$ 个数，$s_0,s_1,\cdots,s_n$，你要让满足 $s_i\neq s_j,i\neq j$ 的无序数对 $(i,j)$ 尽量多

考虑相反的问题，让相同数对尽量少，显然值为 $x$ 的项与值为 $x$ 取反的项无本质区别，我们可以开一个桶将其存起来

显然只有一个桶内的数可能会生成相同数对，可以证明如果 $x$ 桶中有 $a$ 个数，则最终序列中有 $\lfloor\frac a2\rfloor$ 个 $x$，$\lceil\frac a2\rceil$ 个 $x$ 取反是最优的

E

题面

你有一个 $n$ 行 $m$ 列的字符串矩阵，给定一个初始矩阵以及一个目标矩阵，你需要通过操作将初始矩阵变成目标矩阵，每次操作你可以选择两个格子 $A$ 与 $B$，满足 $A$ 中的字符串非空且 $A$ 与 $B$ 有公共行或公共列，并将 $A$ 中字符串的尾部拼接到 $B$ 中字符串的头部，请构造一种方案，要求操作次数小于等于字符串总长的 $4$ 倍，$1\le n,m\le300$

题解

一个简单的想法是将所有 0 聚集到一起，将所有 1 聚集到一起，然后再挨个分配

具体方案：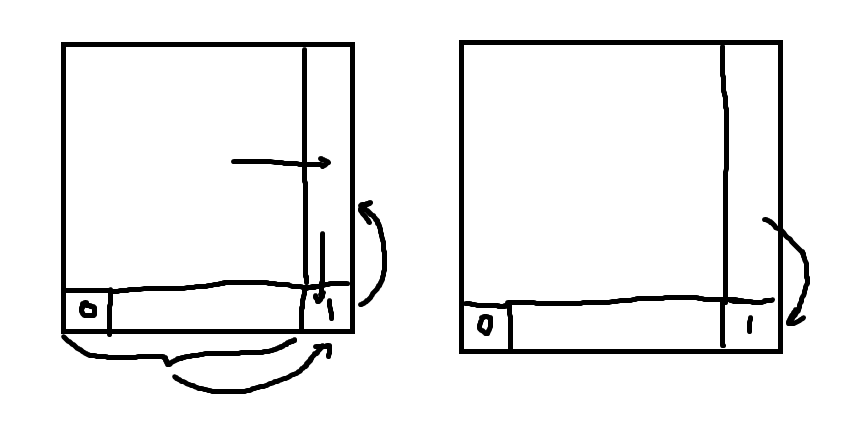

左为第一轮，我们将所有原串中的字符均改变位置，将矩形划分为若干区域，如上移动

右为第二轮，此时我们只需要将剩余的 1 移到右下角即可

0 的情况对称

接下来考虑如何分配

将 $s$ 的最后一个字符放到 $t$ 前，得到 $s^\prime,t^\prime$，相当于将 $t^\prime$ 倒序的最后一个字符放到 $s^\prime$ 倒序前面

那么我们考虑将目标矩阵中的每个字符串倒序，然后再将其变为左下角 0，右下角 1，我们将这个操作序列倒序就得到了如何分配

F

题面

平面直角坐标系上有两种电线，一种是红线，连接 $y$ 相同的点，一种是蓝线，连接 $x$ 相同的点，可以出现自环，自环可以为蓝或红

同色的电线没有重合部分，异色电线恰好有 $n$ 个交点 $(x_i,y_i)$，请构造一种使用电线数最少且符合要求的连接方案，$1\le n\le1000$

题解

考虑电线两端一定是交点最优，我们可以先将每个点连两个自环，在这个基础上尽可能地去省电线

我们可以对于每一个 $x$ 坐标，连接一些相邻点之间的电线，最后把连续的电线合并到一起，达到省电线的目的，对 $y$ 坐标同样处理

显然这样我们保证了异色相交的点都满足条件，接下来需要保证的就是中间不出现多余的交点，那么我们就会得到若干“某红线不能与某蓝线同时存在”，而红蓝内部没有这类要求，这是二分图最大独立集问题，网络流解决即可